
【题目】如图1,把一张长方形的纸片ABCD沿对角线BD折叠,点C落在E处,BE交AD于点F. 
(1)求证:FB=FD;
(2)如图2,连接AE,求证:AE∥BD; 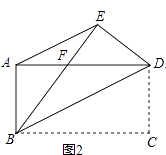
(3)如图3,延长BA,DE相交于点G,连接GF并延长交BD于点H,求证:GH垂直平分BD. 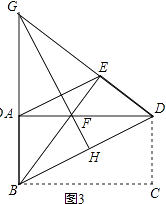
【答案】
(1)证明:∵△BCD≌△BED,
∴∠DBC=∠EBD,
又∵四边形ABCD是长方形,
∴AD∥BC,
∴∠ADB=∠DBC,
∴∠ADB=∠EBD,
∴BF=DF.
(2)证明:∵四边形ABCD是长方形,
∴AD=BC=BE,
又∵FB=FD,
∴FA=FE,
∴∠FAE=∠FEA,
又∵∠AFE=∠BFD,且2∠AEF+∠AFE=2∠FBD+∠BFD=180°,
∴∠AEF=∠FBD,
∴AE∥BD;
(3)证明:∵四边形ABCD是长方形,
∴AD=BC=BE,AB=CD=DE,BD=DB,
在△ABD与△EDB中,
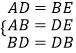
∴△ABD≌△EDB(SSS),
∴∠ABD=∠EDB,
∴GB=GD,
又∵FB=FD,
∴GF是BD的垂直平分线,即GH垂直平分BD.
【解析】(1)由折叠的性质可得到△ABD≌△EDB,那么∠ADB=∠EBD,所以BF=DF;(2)根据长方形的性质可得和三角形内角和定理可得∠AEF=∠FBD,再根据平行线的判定即可求解;(3)先SSS证明△ABD≌△EDB,再根据全等三角形的性质和垂直平分线的性质即可求解.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】学之道在于悟.希望同学们在问题(1)解决过程中有所悟,再继续探索研究问题(2).
(1)如图①,∠B=∠C,BD=CE,AB=DC. ①求证:△ADE为等腰三角形.
②若∠B=60°,求证:△ADE为等边三角形.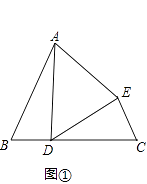
(2)如图②,射线AM与BN,MA⊥AB,NB⊥AB,点P是AB上一点,在射线AM与BN上分别作点C、点 D 满足:△CPD为等腰直角三角形.(要求:利用直尺与圆规,不写作法,保留作图痕迹) 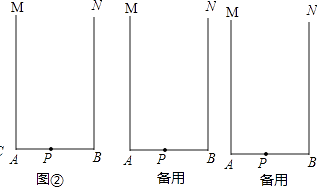
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺指针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…,若点A(![]() ,0),B(0,4),则点B2016的横坐标为( )
,0),B(0,4),则点B2016的横坐标为( )
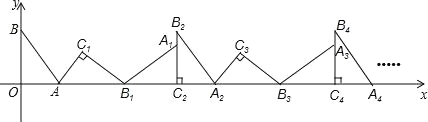
A.5 B.12 C.10070 D.10080
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com