练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知|x+1|+（y﹣2）2=0，求﹣[（﹣3x2y2+3x2y）+3x2y2﹣3xy2）]的值

    【答案】解：由已知得 解得，x=-1，y=2．

    原式=﹣[（﹣3x2y2+3x2y）+3x2y2﹣3xy2）]=3xy2-3x2y=3×（-1）×22-3×（-1）2×2=-18．


    【解析】先根据几个非负数之和为0，则每一个非负数都为0，建立方程组求出x、y的值，再将代数式去括号，合并同类项，结果化成最简，然后代入求值即可。
    【考点精析】掌握解一元一次方程的步骤和代数式求值是解答本题的根本，需要知道先去分母再括号，移项变号要记牢．同类各项去合并，系数化“1”还没好．求得未知须检验，回代值等才算了；求代数式的值，一般是先将代数式化简，然后再将字母的取值代入；求代数式的值，有时求不出其字母的值，需要利用技巧，“整体”代入．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一次智力测验,有20道选择题.评分标准是:对1题给5分,错1题扣2分,不答题不给分也不扣分.小明有两道题未答.至少答对几道题,总分才不会低于60分.则小明至少答对的题数是( )

    A.11道 B。12题 C.13题 D.14题

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，把一张长方形的纸片ABCD沿对角线BD折叠，点C落在E处，BE交AD于点F．
    （1）求证：FB=FD；
    （2）如图2，连接AE，求证：AE∥BD；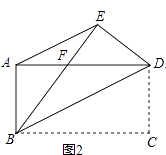
    （3）如图3，延长BA，DE相交于点G，连接GF并延长交BD于点H，求证：GH垂直平分BD．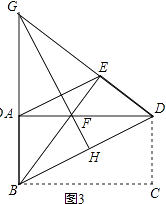

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰直角△ABC中，∠ACB=90°，CO⊥AB于点O，点D、E分别在边AC、BC上，且AD=CE，连结DE交CO于点P，给出以下结论：

    ①△DOE是等腰直角三角形；②∠CDE=∠COE；③若AC=1，则四边形CEOD的面积为；④，其中所有正确结论的序号是 ．

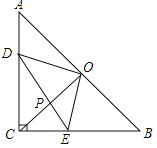
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线MN是四边形AMBN的对称轴，点P是直线MN上的点，给出下列判断： ①AM=BM；②AP=BN；③∠MAP=∠MBP；④AN∥BP．其中结论正确的是：（填上序号即可）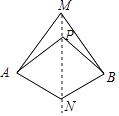

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC＝120°．将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．将图1中的三角板绕点O逆时针旋转至图2，使一边OM在∠BOC的内部，另一边ON仍在直线AB的下方．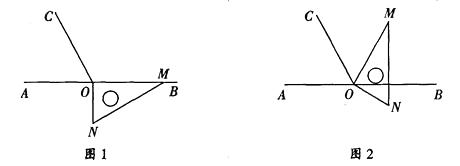

    （1）若OM恰好平分∠BOC，求∠BON的度数；
    （2）若∠BOM等于∠COM余角的3倍，求∠BOM的度数；
    （3）若设∠BON＝α（0°<α<90°），试用含α的代数式表示∠COM．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

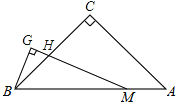
    【题目】如图，△ABC中，∠C=90°，CA=CB，点M在线段AB上，∠GMB=∠A，BG⊥MG，垂足为G，MG与BC相交于点H．若MH=8cm，则BG= cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】据图回答下列问题

    （1）数轴上表示5与﹣2两点之间的距离是 ，
    （2）数轴上表示x与2的两点之间的距离可以表示为 ．
    （3）如果|x﹣2|=5，则x= ．
    （4）同理|x+3|+|x﹣1|表示数轴上有理数x所对应的点到﹣3和1所对应的点的距离之和，请你找出所有符合条件的整数x，使得|x+3|+|x﹣1|=4，这样的整数是 ．
    （5）由以上探索猜想对于任何有理数x，|x﹣3|+|x﹣6|是否有最小值？如果有，直接写出最小值；如果没有，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知a，b是一个等腰三角形的两边长，且满足a2＋b2－4a－6b＋13＝0，求这个等腰三角形的周长．

    查看答案和解析>>

    同步练习册答案