
【题目】如图,四边形ABCD中,AE平分∠BAD,DE平分∠ADC. 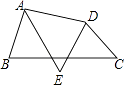
(1)如果∠B+∠C=120°,则∠AED的度数= . (直接写出结果)
(2)根据(1)的结论,猜想∠B+∠C与∠AED之间的关系,并证明.
【答案】
(1)60°
(2)解:∠AED= ![]() (∠B+∠C).
(∠B+∠C).
理由如下:在四边形ABCD中,
∵∠BAD+∠CDA+∠B+∠C=360°,
∴∠BAD+∠CDA=360°﹣(∠B+∠C),
又∵AE平分∠BAD,DE平分∠ADC,
∴∠EAD= ![]() ∠BAD,∠EDA=
∠BAD,∠EDA= ![]() ∠ADC,
∠ADC,
∴∠EAD+∠EDA= ![]() ∠BAD+
∠BAD+ ![]() ∠ADC=
∠ADC= ![]() [360°﹣(∠B+∠C)],
[360°﹣(∠B+∠C)],
在△AED中,又∵∠AED=180°﹣(∠EAD+∠EDA),
=180°﹣ ![]() [360°﹣(∠B+∠C)],
[360°﹣(∠B+∠C)],
= ![]() (∠B+∠C),
(∠B+∠C),
故∠AED= ![]() (∠B+∠C).
(∠B+∠C).
【解析】解:(1)在四边形ABCD中,∵∠B+∠C=120°, ∴∠BAD+∠CDA=360°﹣120°=240°,
∵AE平分∠BAD,DE平分∠ADC,
∴∠EAD= ![]() ∠BAD,∠EDA=
∠BAD,∠EDA= ![]() ∠ADC,
∠ADC,
∴∠EAD+∠EDA= ![]() ∠BAD+
∠BAD+ ![]() ∠ADC=
∠ADC= ![]() (∠BAD+∠CDA)=
(∠BAD+∠CDA)= ![]() ×240°=120°,
×240°=120°,
在△AED中,∠AED=180°﹣(∠EAD+∠EDA),
=180°﹣120°,
=60°;
所以答案是:60°.
【考点精析】本题主要考查了多边形内角与外角的相关知识点,需要掌握多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D. 
(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).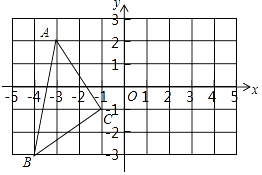
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点C1的坐标(直接写答案):C1;
(3)△A1B1C1的面积为;
(4)在y轴上画出点P,使PB+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.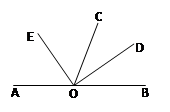
(1)指出图中∠AOD与∠BOE的补角;
(2)试判断∠COD与∠COE具有怎样的数量关系.并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学之道在于悟.希望同学们在问题(1)解决过程中有所悟,再继续探索研究问题(2).
(1)如图①,∠B=∠C,BD=CE,AB=DC. ①求证:△ADE为等腰三角形.
②若∠B=60°,求证:△ADE为等边三角形.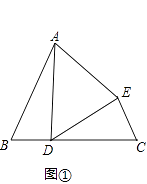
(2)如图②,射线AM与BN,MA⊥AB,NB⊥AB,点P是AB上一点,在射线AM与BN上分别作点C、点 D 满足:△CPD为等腰直角三角形.(要求:利用直尺与圆规,不写作法,保留作图痕迹) 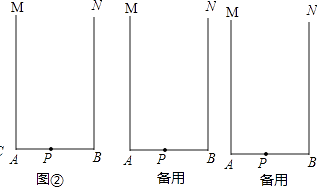
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在长和宽分别是 ![]() 、
、 ![]() 的矩形纸片的四个角上都剪去一个边长为
的矩形纸片的四个角上都剪去一个边长为 ![]() 的小正方形,折成一个无盖的纸盒.
的小正方形,折成一个无盖的纸盒.
(1)用a , b , x表示纸片剩余部分的面积;
(2)当a=16,b=12,且剪去部分的面积等于剩余部分的面积的一半时,求小正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙两人均从400米的环形跑道的A处出发,各自以每秒6米和每秒8米的速度在跑道上跑步.
(1)若两人同时出发,背向而行,则经过秒钟两人第一次相遇;
若两人同时出发,同向而行,则经过秒钟乙第一次追上甲.
(2)若两人同向而行,乙在甲出发10秒钟后去追甲,经过多少时间乙第二次追上甲.
(3)若让甲先跑10秒钟后乙开始跑,在乙用时不超过100秒的情况下,乙跑多少秒钟时,两人相距40米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com