
【题目】如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.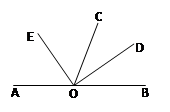
(1)指出图中∠AOD与∠BOE的补角;
(2)试判断∠COD与∠COE具有怎样的数量关系.并说明理由.
【答案】
(1)解:因为∠AOD+∠BOD=180,
所以∠AOD的补角为∠BOD,
又因为OD平分∠BOC,
所以∠COD=∠BOD,
所以∠AOD的补角为∠BOD,∠COD;
同理因为∠AOE+∠BOE=180,
所以∠BOE的补角为∠AOE,
又因为OE平分∠AOC,
所以∠COE=∠AOE,
所以∠BOE的补角为∠AOE,∠COE
(2)解:∵OD平分∠BOC,OE平分∠AOC,
∴∠COE= ![]() ∠AOC,∠COD=
∠AOC,∠COD= ![]() ∠BOC,
∠BOC,
∴∠COD+∠COE= ![]() ∠BOC+
∠BOC+ ![]() ∠AOC=
∠AOC= ![]() ∠AOB=90,
∠AOB=90,
即∠COD与∠COE的数量关系是∠COD+∠COE=90
【解析】 (1)根据已知和图形可知∠AOD+∠BOD=180,∠AOE+∠BOE=180,再根据角平分线的定义得出∠COD=∠BOD,∠COE=∠AOE,即可得出图中∠AOD与∠BOE的补角。
(2)根据角平分线的定义,可得出∠COE与∠AOC的数量关系,∠COD与∠BOC的数量关系,再求出∠COD与∠COE的和,即可得出结论。


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】课本中有一个例题:
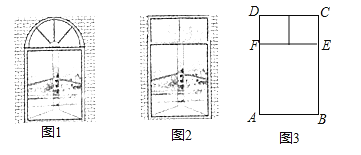
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2.
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题:
(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
根据联合国《人口老龄化及其社会经济后果》中提到的标准,当一个国家或地区65岁及以上老年人口数量占总人口比例超过7%时,意味着这个国家或地区进入老龄化。从经济角度,一般可用“老年人口抚养比”来反映人口老龄化社会的后果。所谓“老年人口抚养比”是指某范围人口中,老年人口数(65岁及以上人口数)与劳动年龄人口数(15-64岁人口数)之比,通常用百分比表示,用以表明每100名劳动年龄人口要负担多少名老年人。
以下是根据我国近几年的人口相关数据制作的统计图和统计表。
2011-2014年全国人口年龄分布图

2011-2014年全国人口年龄分布表
2011年 | 2012年 | 2013年 | 2014年 | |
0-14岁人口占总人口的百分比 | 16.4% | 16.5% | 16.4% | 16.5% |
15-64岁人口占总人口的百分比 | 74.5% | 74.1% | 73.9% | 73.5% |
65岁及以上人口占总人口的百分比 | m | 9.4% | 9.7% | 10.0% |
*以上图表中数据均为年末的数据。
根据以上材料解答下列问题:
(1)2011年末,我国总人口约为_______亿,全国人口年龄分布表中m的值为_______;
(2)若按目前我国的人口自然增长率推测,到2027年末我国约有14.60亿人。假设0-14岁人口占总人口的百分比一直稳定在16.5%,15-64岁的人口一直稳定在10亿,那么2027年末我国0-14岁人口约为_______亿,“老年人口抚养比”约为_______; (精确到1%)
(3)2016年1月1日起我国开始施行“全面二孩”政策,一对夫妻可生育两个孩子。在未来10年内,假设出生率显著提高,这_______(填“会”或“不会”)对我国的“老年人口抚养比”产生影响。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列两点中,关于y轴对称的是( )
A. (1,-3)和(-1,3) B. (3,-5)和(-5,3) C. (5,-4)和(5,4) D. (-2,4)和(2,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AE平分∠BAD,DE平分∠ADC. 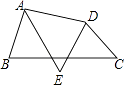
(1)如果∠B+∠C=120°,则∠AED的度数= . (直接写出结果)
(2)根据(1)的结论,猜想∠B+∠C与∠AED之间的关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电厂有5000吨电煤.
(1)求:这些电煤能够使用的天数x(单位:天)与该厂平均每天用煤吨数y(单位:吨)之间的函数关系;
(2)若平均每天用煤200吨,则这批电煤能用多少天?
(3)若该电厂前10天每天用200吨,后因各地用电紧张,每天用电煤300吨,则这批电煤共可用多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是高,E、F分别是AB、AC的中点. 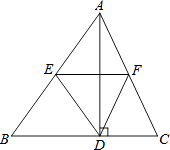
(1)若AB=10,AC=8,求四边形AEDF的周长;
(2)求证:EF垂直平分AD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com