练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，在长和宽分别是 、 的矩形纸片的四个角上都剪去一个边长为 的小正方形，折成一个无盖的纸盒．

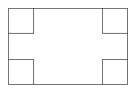
    （1）用a ， b ， x表示纸片剩余部分的面积；
    （2）当a=16，b=12，且剪去部分的面积等于剩余部分的面积的一半时，求小正方形的边长．

    【答案】
    （1）解：ab-4x2
    （2）解：4x2=0.5(ab-4x2 )

    6x =0.5×16×12

    x=4.
    答：小正方形的边长为4.


    【解析】（1）用全面积减去四个小正方形的面积即可得出剩余面积；
    （2）由“剪去部分的面积等于剩余部分的面积的一半”可得到等式，再把a、b的值代入，从而求得x的值，即可得答案.
    【考点精析】关于本题考查的算数平方根，需要了解正数a的正的平方根叫做a的算术平方根；正数和零的算术平方根都只有一个，零的算术平方根是零才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一茶叶专卖店经销某种品牌的茶叶，该茶叶的成本价是80元/kg，销售单价不低于120元/kg．且不高于180元/kg，经销一段时间后得到如下数据：

    设y与x的关系是我们所学过的某一种函数关系．

    （1）直接写出y与x的函数关系式，并指出自变量x的取值范围；

    （2）当销售单价为多少时，销售利润最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】课本中有一个例题：

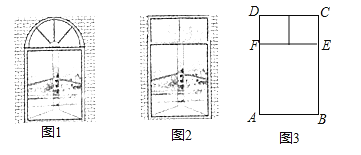
    有一个窗户形状如图1，上部是一个半圆，下部是一个矩形，如果制作窗框的材料总长为6m，如何设计这个窗户，使透光面积最大？

    这个例题的答案是：当窗户半圆的半径约为0.35m时，透光面积最大值约为1.05m2．

    我们如果改变这个窗户的形状，上部改为由两个正方形组成的矩形，如图2，材料总长仍为6m，利用图3，解答下列问题：

    （1）若AB为1m，求此时窗户的透光面积？

    （2）与课本中的例题比较，改变窗户形状后，窗户透光面积的最大值有没有变大？请通过计算说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列两点中，关于y轴对称的是（ ）

    A. (1,-3)和(-1,3) B. (3,-5)和(-5,3) C. (5,-4)和(5,4) D. (-2，4)和（2,4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，AE平分∠BAD，DE平分∠ADC．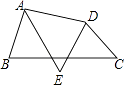
    （1）如果∠B+∠C=120°，则∠AED的度数= ． （直接写出结果）
    （2）根据（1）的结论，猜想∠B+∠C与∠AED之间的关系，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

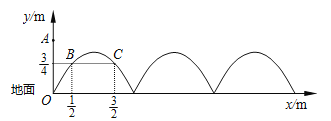
    【题目】如图，需在一面墙上绘制几个相同的抛物线型图案．按照图中的直角坐标系，最左边的抛物线可以用（a≠0）表示．已知抛物线上B，C两点到地面的距离均为m，到墙边OA的距离分别为m，m．

    （1）求该拋物线的函数关系式，并求图案最高点到地面的距离；

    （2）若该墙的长度为10m，则最多可以连续绘制几个这样的拋物线型图案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某电厂有5000吨电煤．

    (1)求：这些电煤能够使用的天数x(单位：天)与该厂平均每天用煤吨数y(单位：吨)之间的函数关系；

    (2)若平均每天用煤200吨，则这批电煤能用多少天？

    (3)若该电厂前10天每天用200吨，后因各地用电紧张，每天用电煤300吨，则这批电煤共可用多少天？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】多项式x2﹣mxy+9y2能用完全平方因式分解，则m的值是（　　）
    A.3
    B.6
    C.±3
    D.±6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把195张图片平均分给若干名学生，已知每人分得的图片数比人数少2．学生有多少人？

    查看答案和解析>>

    同步练习册答案