
【题目】已知甲、乙两人均从400米的环形跑道的A处出发,各自以每秒6米和每秒8米的速度在跑道上跑步.
(1)若两人同时出发,背向而行,则经过秒钟两人第一次相遇;
若两人同时出发,同向而行,则经过秒钟乙第一次追上甲.
(2)若两人同向而行,乙在甲出发10秒钟后去追甲,经过多少时间乙第二次追上甲.
(3)若让甲先跑10秒钟后乙开始跑,在乙用时不超过100秒的情况下,乙跑多少秒钟时,两人相距40米.
【答案】
(1)![]()
![]() ,200
,200
(2)解:设经过x秒时乙第二次追上甲,
则8x-6x=400+6×10,
x=230(秒)
(3)解:设经过x秒时甲乙两人相距40米,
同向而行时(甲在前乙在后)60+6x-8x=40,x =10(秒);
(乙超过甲后)8x-(60+6x)=40,x=50(秒);
相向而行时(相遇前)60+6x+8x=360,x = ![]() (秒);
(秒);
(相遇后)60+6x+8x=440, x= ![]() (秒)
(秒)
【解析】解:(1)两人同时出发,背向而行,两人第一次相遇需要:400÷(8+6)=![]() (秒),
(秒),
两人同时出发,同向而行,两人第一次相遇需要:400÷(8-6)=200(秒);
(1)根据两人同时出发,背向而行,两人第一次相遇时,两人所行的路程之和为环形路程;两人同时出发,同向而行,两人第一次相遇,两人所行的路程之差为环形路程,再由时间等于路程除以速度可求出答案;
(2)设经过x秒时乙第二次追上甲,根据甲乙所行的路程之差=环形路程+甲提前跑的路程来解方程求解;
(3)设经过x秒时甲乙两人相距40米,分两人同向和背向而行来讨论求解.当同向而行时,再分甲在前乙在后和乙超过甲后列方程求解;相向而行时,分相遇前和相遇后来列方程求解.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AE平分∠BAD,DE平分∠ADC. 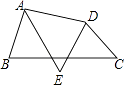
(1)如果∠B+∠C=120°,则∠AED的度数= . (直接写出结果)
(2)根据(1)的结论,猜想∠B+∠C与∠AED之间的关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电厂有5000吨电煤.
(1)求:这些电煤能够使用的天数x(单位:天)与该厂平均每天用煤吨数y(单位:吨)之间的函数关系;
(2)若平均每天用煤200吨,则这批电煤能用多少天?
(3)若该电厂前10天每天用200吨,后因各地用电紧张,每天用电煤300吨,则这批电煤共可用多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次智力测验,有20道选择题.评分标准是:对1题给5分,错1题扣2分,不答题不给分也不扣分.小明有两道题未答.至少答对几道题,总分才不会低于60分.则小明至少答对的题数是( )
A.11道 B。12题 C.13题 D.14题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是高,E、F分别是AB、AC的中点. 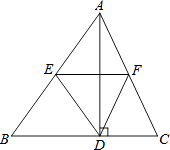
(1)若AB=10,AC=8,求四边形AEDF的周长;
(2)求证:EF垂直平分AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,另一边ON仍在直线AB的下方.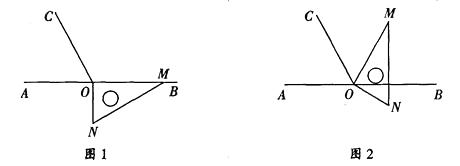
(1)若OM恰好平分∠BOC,求∠BON的度数;
(2)若∠BOM等于∠COM余角的3倍,求∠BOM的度数;
(3)若设∠BON=α(0°<α<90°),试用含α的代数式表示∠COM.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com