练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】① 如图，由小正方形组成的L形图中，用三种方法分别在图中添一个小正方形使图形成为轴对称图形：

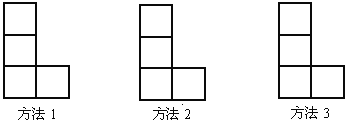
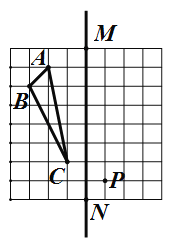
    ② 如图，在正方形网格上的一个△ABC．

    ⑴ 作△ABC关于直线MN的对称图形(不写作法)；

    ⑵ 以P为一个顶点作与△ABC全等的三角形（规定点P与点B对应，另两顶点都在图中网格交点处)，则可作出 个三角形与△ABC全等．

    【答案】①作图见解析；②（1）作图见解析；(2)3个.

    【解析】试题分析：①直接利用轴对称图形的性质得出答案；

    ②（1）直接利用轴对称图形的性质得出对应点位置进而得出答案；

    （2）直接利用网格结合全等三角形的性质得出答案．

    试题解析：①如图1所示：即为所求；

    ②（1）如图2所示：△A′B′C′即为所求；

    （2）如图所示：3个三角形与△ABC全等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知点A在x轴上方，y轴左侧，到x轴的距离是3，到y轴的距离是4，那么点A的坐标是______________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知正比例函数y=（4m+6）x ， 当m 时，函数图象经过第二、四象限．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若一个多边形的每个外角都等于60°，则它的内角和等于（ ）
    A.180°
    B.720°
    C.1080°
    D.540°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某人存入5000元参加三年期教育储蓄(免征利息税)，本息共得5417元，那么这种储蓄的年利率为

    A．2．22%B．2．58%C．2．78% D．2．38%

    查看答案和解析>>

    科目：初中数学 来源： 题型：

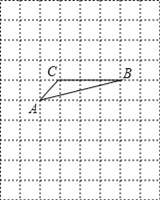
    【题目】如图，将△ABC放在每个小正方形的边长为1的网格中，点A，点B，点C均落在格点上．

    （Ⅰ）计算AC2+BC2的值等于　　　　　　；

    （Ⅱ）请在如图所示的网格中，用无刻度的直尺，画出一个以AB为一边的矩形，使该矩形的面积等于AC2+BC2，并简要说明画图方法（不要求证明）　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

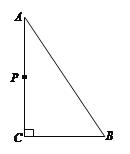
    【题目】如图，△ABC中，∠C=90°，AB=5cm，BC=3cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm，设出发的时间为t秒．

    （1）若点P恰好在∠BAC的角平分线上，求t的值；

    （2）问t为何值时，△BCP为等腰三角形？

    （3）另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒2cm，若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动．当t为何值时，直线PQ把△ABC的周长分成相等的两部分？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个多项式与3m2 4 的和是m2 m 5 ，则这个多项式为（ ）

    A. 2m2 m 9 B. 2m2 m 1

    C. 2m2 m 9 D. 2m2 m 9

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在等腰直角△ABC中，AB=AC，∠BAC=90°，小敏将一块三角板中含45°角的顶点放在A上，从AB边开始绕点A逆时针旋转一个角α，其中三角板斜边所在的直线交直线BC于点D，直角边所在的直线交直线BC于点E．

    （1）小敏在线段BC上取一点M，连接AM，旋转中发现：若AD平分∠BAM，则AE也平分∠MAC．请你证明小敏发现的结论；

    （2）当0°＜α≤45°时，小敏在旋转中还发现线段BD、CE、DE之间存在如下等量关系：BD2+CE2=DE2．同组的小颖和小亮随后想出了相同的方法进行解决：将△ABD沿AD所在的直线对折得到△ADF（如图2）；请证明小敏的发现的是正确的．

    查看答案和解析>>

    同步练习册答案