
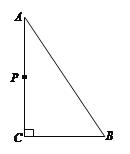
【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)若点P恰好在∠BAC的角平分线上,求t的值;
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
【答案】(1)![]() ;(2)3s、5.4s、6s、6.5s;(3)2或6秒
;(2)3s、5.4s、6s、6.5s;(3)2或6秒
【解析】试题分析:(1)过P作PE⊥AB,设CP=2t,根据角平分线的性质和勾股定理进行解答即可;
(2)分类讨论:当CP=CB时,△BCP为等腰三角形,若点P在AC上得t=3(s),若点P在AB上,则t=5.4s;当PC=PB时,△BCP为等腰三角形,作PD⊥BC于D,根据等腰三角形的性质得BD=CD,则可判断PD为△ABC的中位线,则AP=![]() AB=
AB=![]() ,易得t=
,易得t=![]() (s);当BP=BC=3时,△BCP为等腰三角形,则AP=AB-BP=2,易得t=6(s);
(s);当BP=BC=3时,△BCP为等腰三角形,则AP=AB-BP=2,易得t=6(s);
(3)分两种情况讨论:当P点在AC上,Q在AB上,则PC=t,BQ=2t-3,t+2t-3+3=6;当P点在AB上,Q在AC上,则AC=t-4,AQ=2t-8,t-4+2t-8=6,分别求得t的值即可.
试题解析:(1)如图1,过P作PE⊥AB,
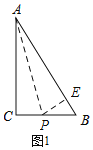
∵点P恰好在∠BAC的角平分线上,且∠C=90°,AB=5cm,BC=3cm,
∴CP=EP,
∴△ACP≌△AEP(HL),
∴AC=4cm=AE,BE=5-4=1,
设CP=x,则BP=3-x,PE=x,
∴Rt△BEP中,BE2+PE2=BP2,
即12+x2=(3-x)2
解得x=![]() ,
,
∴BP=3-![]() =
=![]() ,
,
∴CA+AB+BP=4+5+![]() =
=![]() ,
,
∴t=![]() ÷1=
÷1=![]() (s);
(s);
(2)如图2,当CP=CB时,△BCP为等腰三角形,
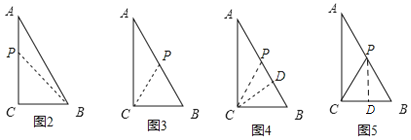
若点P在CA上,则1t=3,
解得t=3(s);
如图3,当BP=BC=3时,△BCP为等腰三角形,
∴AP=AB-BP=2,
∴t=(4+2)÷1=6(s);
如图4,若点P在AB上,CP=CB=3,作CD⊥AB于D,则根据面积法求得CD=![]() ,
,
在Rt△BCD中,由勾股定理得,BD=![]() ,
,
∴PB=2BD=![]()
∴CA+AP=4+5-![]() =5.4,
=5.4,
此时t=5.4÷1=5.4(s);
如图5,当PC=PB时,△BCP为等腰三角形,作PD⊥BC于D,则BD=CD,
∴PD为△ABC的中位线,
∴AP=BP=![]() AB=
AB=![]() ,
,
∴t=(4+![]() )÷1=
)÷1=![]() (s);
(s);
综上所述,t为3s或5.4s或6s或![]() s时,△BCP为等腰三角形;
s时,△BCP为等腰三角形;
(3)如图6,当P点在AC上,Q在AB上,则PC=t,BQ=2t-3,
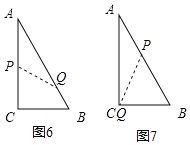
∵直线PQ把△ABC的周长分成相等的两部分,
∴t+2t-3+3=6,
∴t=2(s);
如图7,当P点在AB上,Q在AC上,则AP=t-4,AQ=2t-8,
∵直线PQ把△ABC的周长分成相等的两部分,
∴t-4+2t-8=6,
∴t=6(s);
综上所述,当t=2或6秒时,直线PQ把△ABC的周长分成相等的两部分.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90,点D为AB边上的一点,
(1)试说明:∠EAC=∠B ;(2)若AD=10,BD=24,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
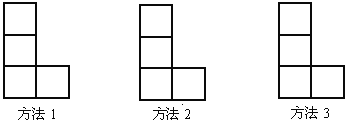
【题目】① 如图,由小正方形组成的L形图中,用三种方法分别在图中添一个小正方形使图形成为轴对称图形:
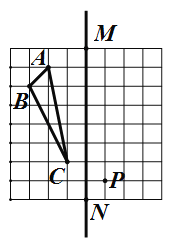
② 如图,在正方形网格上的一个△ABC.
⑴ 作△ABC关于直线MN的对称图形(不写作法);
⑵ 以P为一个顶点作与△ABC全等的三角形(规定点P与点B对应,另两顶点都在图中网格交点处),则可作出 个三角形与△ABC全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为______cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个相似三角形的对应边分别是15cm和25cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
A.75cm,115cmB.60cm,100cmC.85cm,125cmD.45cm,85cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com