
【题目】如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90,点D为AB边上的一点,
(1)试说明:∠EAC=∠B ;(2)若AD=10,BD=24,求DE的长.

【答案】(1)见解析;(2)DE=26
【解析】试题分析:(1)由于△ACB与△ECD都是等腰直角三角形,CD=CE,CB=CA,∠B=∠CAB=45°,∠ACB=∠ECD=90°,于是∠ACE+∠ACD=∠ACD+∠BCD,根据等式性质可得∠ACE=∠BCD,利用SAS可证△ACE≌△BCD,利用全等三角形的对应角相等即可解答;
(2)根据△ACE≌△BCD,于是∠EAC=∠B=45°,AE=BD=24,易求∠EAD=90°,再利用勾股定理可求DE=26.
解:(1)∵∠ACB=∠ECD=90°,
∴∠ACB﹣∠ACD=∠ECD﹣∠ACD,
∴∠ECA=∠DCB,
∵△ACB和△ECD都是等腰三角形,
∴EC=DC,AC=BC,
在△ACE和△BCD中,
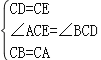 ,
,
∴△ACE≌△BCD,
∴∠EAC=∠B.
(2)∵△ACE≌△BCD,
∴AE=BD=24,
∵∠EAC=∠B=45°
∴∠EAD=∠EAC+∠CAD=90°,
∴在Rt△ADE中,DE2=EA2+AD2,
∴DE2=102+242,
∴DE=26.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
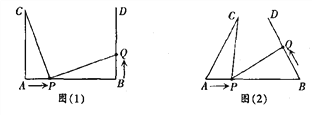
【题目】如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人存入5000元参加三年期教育储蓄(免征利息税),本息共得5417元,那么这种储蓄的年利率为
A.2.22%B.2.58%C.2.78% D.2.38%
查看答案和解析>>
科目:初中数学 来源: 题型:
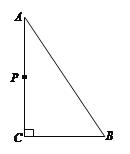
【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)若点P恰好在∠BAC的角平分线上,求t的值;
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com