
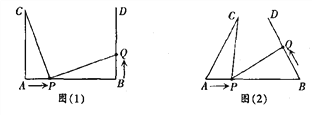
����Ŀ����ͼ(1)��AB��4cm��AC��AB��BD��AB��AC��BD��3cm����P���߶�AB����1cm/s���ٶ��ɵ�A���B�˶���ͬʱ����Q���߶�BD���ɵ�B���D�˶��������˶���ʱ��Ϊt(s)��
(1)����Q���˶��ٶ����P���˶��ٶ���ȣ���t��1ʱ����ACP���BPQ�Ƿ�ȫ�ȣ���˵�����ɣ����жϴ�ʱ�߶�PC���߶�PQ��λ�ù�ϵ��
(2)��ͼ(2)����ͼ(1)�еġ�AC��AB��BD��AB��Ϊ�ġ���CAB����DBA��60�㡱�������������䣮���Q���˶��ٶ�Ϊx cm/s���Ƿ����ʵ��x��ʹ�á�ACP���BPQȫ�ȣ������ڣ������Ӧ��x��t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��ȫ�ȣ�PC��PQ�����ɲμ���������2�����ڣ�t=1��x="1" ��t=2��x=![]() ��
��
�������������������1������SAS֤����ACP�ա�BPQ���ó���ACP=��BPQ����һ���ó���APC+��BPQ=��APC+��ACP=90���ó����ۼ��ɣ���2������ACP�ա�BPQ���������������AC=BP��AP=BQ����AC=BQ��AP=BP��������������ô𰸼��ɣ�
�����������1����t=1ʱ��AP=BQ=1����AB��4cm����BP=AC=3������Ϊ��A=��B=90�������ACP�ա�BPQ��SAS�������ACP=��BPQ�����APC+��BPQ=��APC+��ACP=90�������CPQ=90�������߶�PC���߶�PQ��ֱ����2�����Q���˶��ٶ�Ϊx cm/s����BQ=tx�������������������ACP�ա�BPQ����AC=BP��AP=BQ������3=4-t��t=xt����ã�t=1��x=1��������ACP�ա�BQP����AC=BQ��AP=BP������3=xt��t=4-t����ã�t=2��x=![]() ����������������������ʵ��x��ʹ����ACP����BPQȫ�ȣ���ʱ��Ӧ��x��t��ֵΪt=1��x="1" ��t=2��x=
����������������������ʵ��x��ʹ����ACP����BPQȫ�ȣ���ʱ��Ӧ��x��t��ֵΪt=1��x="1" ��t=2��x=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=-x��ͼ��ƽ�֣�������
A.��һ��������
B.��һ��������
C.�ڶ���������
D.�ڶ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������ʽ����3x2y��3xy2��x3��3x2y�����������ʽ�ǣ� ��
A.x3+3xy2
B.x3��3xy2
C.x3��6x2y+3xy2
D.x3��6x2y��3x2y
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y=5x2������ƽ��2����λ��������ƽ��3����λ��õ��µ������ߣ����������ߵı���ʽ�ǣ�������
A.y=5��x+2��2+3
B.y=5��x��2��2+3
C.y=5��x��2��2��3
D.y=5��x+2��2��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˸��õı�������ͼ��������ʪ�أ���������ˮ�����������ȹ���A��B������ˮ�����豸��20̨��������ʪ���ܱ���ˮ���д�����ÿ̨A����ˮ�����豸12��Ԫ��ÿ̨B����ˮ�����豸10��Ԫ����֪1̨A����ˮ�����豸��2̨B����ˮ�����豸ÿ�ܿ��Դ�����ˮ640�֣�2̨A����ˮ�����豸��3̨B����ˮ�����豸ÿ�ܿ��Դ�����ˮ1080����
��1����A��B������ˮ�����豸ÿ�ֱܷ���Դ�����ˮ���ٶ֣�
��2����Ԥ�㣬����ˮ�����������豸���ʽ���230��Ԫ��ÿ�ܴ�����ˮ����������4500�֣������оٳ����й�������ָ�����ַ��������ʽ����٣������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ACB���ECD���ǵ���ֱ�������Σ���ACB����ECD��90����DΪAB���ϵ�һ�㣬
��1����˵������EAC����B ����2����AD��10��BD��24����DE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʡ����ȫ��ҽ���ĸ�3��������Ͷ��36420000000Ԫ������36420000000�ÿ�ѧ��������ʾΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ų�Ϊ8cm����Ϊ6cm�ľ���ֽƬ�ϣ���Ҫ����һ������Ϊ5cm�ĵ��������Σ�Ҫ���������ε�һ����������ε�һ�������غϣ���������������ھ��εı��ϣ�������µĵ��������ε����Ϊ______cm2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�ա�DEF������ABC���ܳ�Ϊ30cm��AB��8cm��BC��12cm����DE��DF�ij��ȷֱ��ǣ� ��
A.8cm��9cmB.8cm��10cmC.10cm��12cmD.8cm��12cm
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com