【题目】一次函数y=-x的图象平分（ ）
A.第一、三象限
B.第一、二象限
C.第二、三象限
D.第二、四象限
优学名师名题系列答案科目：初中数学 来源： 题型：
【题目】勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪灵感.他惊喜地发现：当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明.下面是小聪利用图1证明勾股定理的过程：
将两个全等的直角三角形按图1摆放，其中∠DAB=90°，求证：a2+b2=c2.
证明：连接DB，过点D作BC边上的高DF，则DF=EC=b-a.
∵S四边形ADCB=S△ACD+S△ABC=
b2+ab.
又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b－a)，
∴b2+ab=c2+a(b－a)，
∴a2+b2=c2.
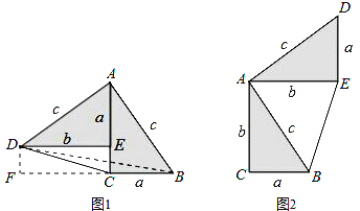
请参照上述证法，利用图2完成下面的证明：
将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°.
求证：a2+b2=c2.
证明：连接 ，
∵S五边形ACBED= ，
又∵S五边形ACBED= ，
∴ ，
∴a2+b2=c2.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1是“东方之星”救援打捞现场图，小红据此构造出一个如图2所示的数学模型，已知：A、B、D三点在同一水平线上，CD⊥AD，∠A=30°，∠CBD=75°，AB=60m．
（1）求点B到AC的距离；
（2）求线段CD的长度．
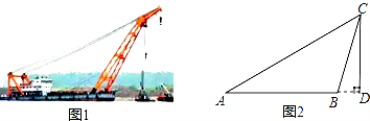
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为节约用水,某市居民生活用水按级收费,具体收费标准如下表：
用水量（吨） | 不超过15吨的部分 | 超过15不超过25吨的部分 | 超过25吨的部分 |
单位（元/吨） | 3 | 5 | 7 |
设李红家某月的为x吨(15<x25)，应付水费为y元，则y关于x的函数表达式为_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】节约是一种美德，节约是一种智慧．据不完全统计，全国每年浪费食物总量折合粮食可养活约3亿5千万人．350 000 000用科学记数法表示为（ ）
A.3.5×107
B.3.5×108
C.3.5×109
D.3.5×1010
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某班12位同学参加每周一次的教室卫生大扫除，有扫地、擦玻璃和擦课桌椅三个项目，扫地的面积为88 m2，擦玻璃的面积为32 m2，根据实际情况将三个项目的面积分配情况和每人每分钟完成各项目的工作量制作如下统计图：
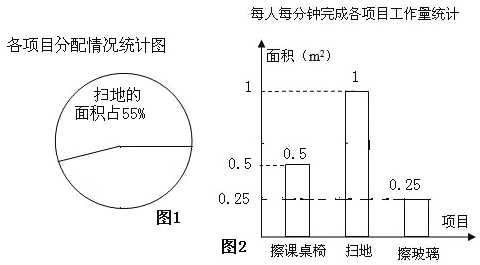
(1)擦课桌椅的面积为__________，请补全图1中的各项目面积分配情况扇形统计图；
(2)卫生委员设计两种方案：
方案一：12位同学先一起完成扫地任务，再一起完成擦玻璃任务，最后一起完成擦课桌椅任务；
方案二：12位同学先一起完成扫地任务后，再把这12位同学分成两组，每组6人，一组擦玻璃，一组去擦课桌椅.
你认为这哪种方案完成大扫除任务所用的时间少，少多少时间？
查看答案和解析>>
科目：初中数学 来源： 题型：
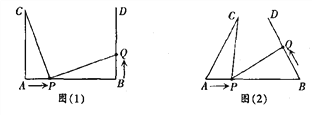
【题目】如图(1)，AB＝4cm，AC⊥AB，BD⊥AB，AC＝BD＝3cm．点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动．它们运动的时间为t(s)．
(1)若点Q的运动速度与点P的运动速度相等，当t＝1时，△ACP与△BPQ是否全等，请说明理由，并判断此时线段PC和线段PQ的位置关系；
(2)如图(2)，将图(1)中的“AC⊥AB，BD⊥AB”为改“∠CAB＝∠DBA＝60°”，其他条件不变．设点Q的运动速度为x cm/s，是否存在实数x，使得△ACP与△BPQ全等？若存在，求出相应的x、t的值；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
