
 如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.分析 (1)连接OD,根据等边对等角得出∠B=∠ODB,∠B=∠C,得出∠ODB=∠C,证得OD∥AC,证得OD⊥DF,从而证得DF是⊙O的切线;
(2)连接BE,AB是直径,∠AEB=90°,根据勾股定理得出BE=2$\sqrt{2}$AE,CE=4AE,然后在RT△BEC中,即可求得tanC的值.
解答 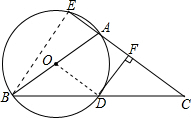 (1)证明:连接OD,
(1)证明:连接OD,
∵OB=OD,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,
∴DF是⊙O的切线;
(2)解:连接BE,
∵AB是直径,
∴∠AEB=90°,
∵AB=AC,AC=3AE,
∴AB=3AE,CE=4AE,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=2$\sqrt{2}$AE,
在RT△BEC中,tanC=$\frac{BE}{CE}$=$\frac{2\sqrt{2}AE}{4AE}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查了等腰三角形的性质,平行线的判定和性质,切线的判定,勾股定理的应用以及直角三角函数等,是一道综合题,难度中等.


科目:初中数学 来源: 题型:选择题
| A. | 20% | B. | 40% | C. | -220% | D. | 30% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
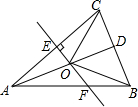 如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
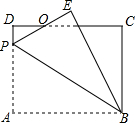 如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为4.8.
如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为4.8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
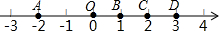 如图,已知数轴上的点A、B、C、D分别表示数-2、1、2、3,则表示数3-$\sqrt{5}$的点P应落在线段( )
如图,已知数轴上的点A、B、C、D分别表示数-2、1、2、3,则表示数3-$\sqrt{5}$的点P应落在线段( )| A. | AO上 | B. | OB上 | C. | BC上 | D. | CD上 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)
北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com