
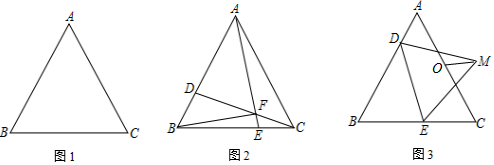
分析 (1)①如图1,由题可得BD=CE=t,易证△BDC≌△CEA,则有∠BCD=∠CAE,根据三角形外角的性质可求得∠EFC=60°,即可得到∠AFC=120°;
②延长FD到G,使得FG=FA,连接GA、GB,根据△FAG是等边三角形,△ABC是等边三角形,即可判定△AGB≌△AFC,从而得出∠BGF=∠EFC=60°,得到EF∥GB,根据平行线分线段成比例定理可得$\frac{CF}{FG}$=$\frac{CE}{EB}$,再根据AF=2CF,CE=t,BC=8,得出GF=2CF,BE=8-t,进而得到$\frac{1}{2}$=$\frac{t}{8-t}$,解得t=$\frac{8}{3}$即可;
(2)连接AM,过D作DH⊥BC于H,根据SAS判定△ADM≌△HED,进而得出∠DAM=∠EHD=90°,而∠DAO=60°,可得∠OAM=90°-60°=30°,因此当OM⊥AM时,OM最短,此时,OM=$\frac{1}{2}$AO,故OM的最小值为2.
解答 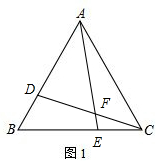 解:(1)①如图1,当a=b=1时,BD=CE=t,
解:(1)①如图1,当a=b=1时,BD=CE=t,
∵△ABC是边长为8cm的等边三角形,
∴CB=AC,∠CBD=∠ACE=60°,
在△BDC和△CEA中,
$\left\{\begin{array}{l}{BD=CE}\\{∠CBD=∠ACE}\\{CB=AC}\end{array}\right.$,
∴△BDC≌△CEA(SAS),
∴∠BCD=∠CAE,
∴∠EFC=∠CAE+∠ACF=∠BCD+∠ACF=∠ACB=60°,
∴∠AFC=120°;
②如图2,延长FD到G,使得FG=FA,连接GA、GB,
∵∠AFG=∠EFC=60°,FG=FA,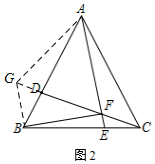
∴△FAG是等边三角形,
∴AG=AF=FG,∠AGF=∠GAF=60°.
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠GAF=∠BAC=60°,
∴∠GAB=∠FAC.
在△AGB和△AFC中,
$\left\{\begin{array}{l}{AG=AF}\\{∠GAB=∠FAC}\\{AB=AC}\end{array}\right.$,
∴△AGB≌△AFC(SAS),
∴∠AGB=∠AFC=120°,
∴∠BGF=60°,
∴∠BGF=∠EFC=60°,
∴EF∥GB,
∴$\frac{CF}{FG}$=$\frac{CE}{EB}$,
又∵AF=2CF,CE=t,BC=8,
∴GF=2CF,BE=8-t,
∴$\frac{1}{2}$=$\frac{t}{8-t}$,
解得t=$\frac{8}{3}$,
∴当AF=2CF时,t的值为$\frac{8}{3}$;
(2)如图3,连接AM,过D作DH⊥BC于H,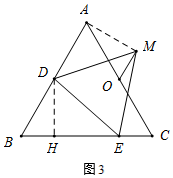
∵当a=2,b=1时,BD=2t,CE=t,而∠B=60°,AB=8,
∴BH=t,AD=8-2t,HE=8-t-t=8-2t,
∴DA=EH,
∵△DEM是等边三角形,
∴DE=MD,∠EDM=60°,
∴∠ADM+∠BDE=∠HED+∠BDE=120°,
∴∠ADM=∠HED,
在△ADM和△HED中,
$\left\{\begin{array}{l}{DA=EH}\\{∠ADM=∠HED}\\{MD=DE}\end{array}\right.$,
∴△ADM≌△HED(SAS),
∴∠DAM=∠EHD=90°,而∠DAO=60°,
∴∠OAM=90°-60°=30°,
∴当OM⊥AM时,OM最短,
∵点O为AC的中点,
∴AO=4,
此时,OM=$\frac{1}{2}$AO=$\frac{1}{2}$×4=2.
故OM的最小值为2.
点评 本题属于三角形综合题,主要考查了等边三角形的性质,全等三角形的判定与性质,平行线分线段成比例定理以及含30°角 的直角三角形的性质的综合应用,解决问题的关键是作辅助线构造等边三角形以及全等三角形,依据全等三角形的对应边相等,对应角相等进行推导计算.解题时注意:在直角三角形中,30°角所对的直角边等于斜边的一半.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:选择题
| A. | 0是代数式 | B. | a是整式 | ||
| C. | x的3倍与y的$\frac{1}{4}$的差表示为3x-$\frac{1}{4}$y | D. | s=πr2是代数式 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
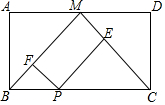 如图所示,点M是矩形ABCD的边AD的中点,P是BC边上一动点,PE⊥MC,PF⊥BM,垂足分别为E,F
如图所示,点M是矩形ABCD的边AD的中点,P是BC边上一动点,PE⊥MC,PF⊥BM,垂足分别为E,F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
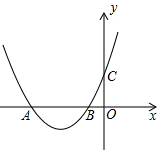 如图,抛物线y=$\frac{1}{8}$x2+3mx+18m2-m与x轴交于A(x1,0),B(x2,0)两点,且x1≠x2,与y轴交于点C.
如图,抛物线y=$\frac{1}{8}$x2+3mx+18m2-m与x轴交于A(x1,0),B(x2,0)两点,且x1≠x2,与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
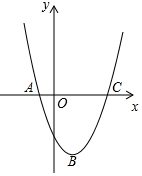 如图,已知二次函数y=x2+bx+c的图象经过点A(-1,0),B(1,-2),与x轴的另一个交点为C.
如图,已知二次函数y=x2+bx+c的图象经过点A(-1,0),B(1,-2),与x轴的另一个交点为C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一个长方形观光园,它的长为100米,宽为50米,在它的四角各建一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)花园种植的是花草,设正方形观光休息亭的边长为x米,则下列说法中错误的是( )
如图,一个长方形观光园,它的长为100米,宽为50米,在它的四角各建一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)花园种植的是花草,设正方形观光休息亭的边长为x米,则下列说法中错误的是( )| A. | 观光园的周长为300米 | B. | 观光休息亭的占地面积为4x2米2 | ||
| C. | 花园占地面积为(100-2x)(50-2x)米2 | D. | 观光大道总长为(300-2x)米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
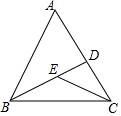 如图,已知在△ABC中,BD是角平分线,点E在BD上,连接CE,若∠BCE=25°,∠CED=55°,则∠ABC的度数为( )
如图,已知在△ABC中,BD是角平分线,点E在BD上,连接CE,若∠BCE=25°,∠CED=55°,则∠ABC的度数为( )| A. | 30° | B. | 40° | C. | 60° | D. | 70° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com