

���� ��1����PΪ���㣬��P��������a�أ�
��2�����Q������Ϊ��xQ��yQ������N������Ϊ��xN��yN���������е���������ʵõ���xN=2xQ-2��yN=2yQ�����ѵ�N���������������c1�Ľ���ʽ�õ�yN=-xN2+8���Ե�N�������ʾ��Q���������������c1�Ľ���ʽ�õ���������c2�Ľ���ʽΪy=-2x2+4x+2��
��3�����A��B������ֱ�ΪA��x1��ax12-4a+4����B��x2��ax22-4a+4������ͼ������B��BG��y�ᣬ����P��PG��x�ᣬBG��PG�ཻ�ڵ�G������A��AH��x�ᣬ����P��PH��y�ᣬAH��PH�ཻ�ڵ�H��ͨ������������Rt��PGB��Rt��AHP�Ķ�Ӧ�߳ɱ����õ� $\frac{BG}{PG}$=$\frac{PH}{AH}$����$\frac{2-{x}_{2}}{a{{x}_{2}}^{2}-4a}$=$\frac{2-{x}_{1}}{-��a{{x}_{1}}^{2}-4a��}$����a��x1+x2��=-4a=2��
��� 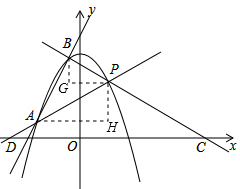 �⣺��1����y=ax2-4a+4=a��x2-4��+4���ú���ͼ�����һ�����ڵĶ���P��
�⣺��1����y=ax2-4a+4=a��x2-4��+4���ú���ͼ�����һ�����ڵĶ���P��
��x2-4=0��
��� x=2��x=-2����ȥ����
��y=4��
���P�������ǣ�2��4����
��2�����Q��������xQ��yQ������N��������xN��yN����
��M��2��0����
�ɵ�Q���߶�MN���е㣬������ã�xN=2xQ-2��yN=2yQ��
��a=-1��
��������c1�Ľ���ʽΪy=-x2+8��
�ߵ�N��������c1�ϣ�
��yN=-xN2+8��
��2yQ=-��2xQ-2��2+8����yQ=-2xQ2+4xQ+2��
��������c2�Ľ���ʽΪ��y=-2x2+4x+2��
��3�����A��B������ֱ�ΪA��x1��ax12-4a+4����B��x2��ax22-4a+4����
�֡ߵ�A��B��ֱ��y=2x+b�ϣ�
��a��x1+x2��=2��
��ͼ������B��BG��y�ᣬ����P��PG��x�ᣬBG��PG�ཻ�ڵ�G������A��AH��x�ᣬ����P��PH��y�ᣬAH��PH�ཻ�ڵ�H��
��PD=PC��
���PDC=��PCD��
��AH��x�ᣬ
���PAH=��PDC��
ͬ������BPG=��PCD��
���AHP=��PGB��
��Rt��PGB��Rt��AHP��
��$\frac{BG}{PG}$=$\frac{PH}{AH}$����$\frac{2-{x}_{2}}{a{{x}_{2}}^{2}-4a}$=$\frac{2-{x}_{1}}{-��a{{x}_{1}}^{2}-4a��}$��
��x1+x2=-4��
��a=-$\frac{1}{2}$��
���� �����ۺϿ����˴���ϵ��������κ�������ʽ�����������ε��ж��������Լ����κ���ͼ���ϵ���������������2����ļ����������õ�Q�������ʾ��N�����꣬Ȼ��ѵ�N��������������������ߵĽ���ʽ��ͨ������������������c2�Ľ���ʽ��


 ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
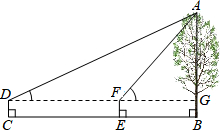 ��ͼ��С��ͬѧ����������һ�ô���AB�ĸ߶ȣ���C����á�ADG=30�㣬��E����á�AFG=60�㣬CE=8�ף������߶�CD=1.4�ף�
��ͼ��С��ͬѧ����������һ�ô���AB�ĸ߶ȣ���C����á�ADG=30�㣬��E����á�AFG=60�㣬CE=8�ף������߶�CD=1.4�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 2.5 | C�� | 3 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | Ϊ�˽���������ѧ����˯�������Ӧ�ò����ղ�ķ�ʽ | |
| B�� | ij�ֲ�Ʊ���н�������1%������100�����ֲ�Ʊһ�����н� | |
| C�� | һ������1��5��3��2��3��4��8����������λ������3 | |
| D�� | ���������ݵķ���s��2=0.1���������ݵķ���s��2=0.2�����������ݱȼ��������ȶ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10 | B�� | 2 | C�� | $\sqrt{10}$ | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com