
【题目】问题情境:如图1,AB∥CD,∠PAB=135°,∠PCD=125°.求∠APC度数.小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可求得∠APC的度数.请写出具体求解过程.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.


【答案】问题情境:100°;问题迁移:(1)∠CPD=∠α+∠β,理由见解析;(2)∠CPD=∠α-∠β或∠CPD=∠α-∠β
【解析】
问题情境:过P作PE∥AB,构造同旁内角,通过平行线性质,可得∠APC=45°+55°=100°;
问题迁移:
(1)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案;
(2)画出图形(分两种情况:①点P在BA的延长线上,②点P在AB的延长线上),根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.
问题情境:过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠APE=180°-∠PAB=180°-135![]() =45°,
=45°,
∠CPE=180°-∠PCD=180°-125![]() =55°,
=55°,
∴∠APC=45°+55°=100°,
故答案为:100°;
问题迁移:
(1)∠CPD=∠α+∠β,理由如下:
如图3,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;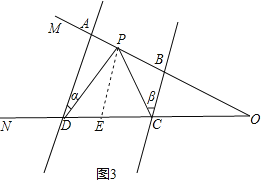
(2)当P在BA延长线时,∠CPD=∠β-∠α;
理由:如图4,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠CPE-∠DPE=∠β-∠α;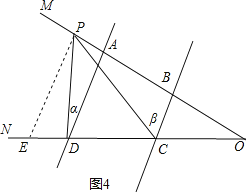
当P在BO之间时,∠CPD=∠α-∠β.
理由:如图5,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE-∠CPE=∠α-∠β.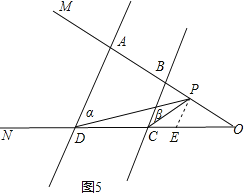


科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AB=2,以点A为圆心,AB为半径的圆交边BC于点E,连接DE、AC、AE.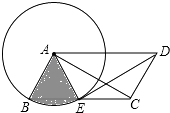
(1)求证:△AED≌△DCA;
(2)若DE平分∠ADC且与⊙A相切于点E,求图中阴影部分(扇形)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学活动中,检验两条纸带①、②的边线是否平行,小明和小丽采用两种不同的方法:小明对纸带①沿AB折叠,量得∠1=∠2=50°;小丽对纸带②沿GH折叠,发现GD与GC重合,HF与HE重合. 则下列判断正确的是( )
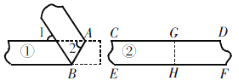
A. 纸带①的边线平行,纸带②的边线不平行 B. 纸带①、②的边线都平行
C. 纸带①的边线不平行,纸带②的边线平行 D. 纸带①、②的边线都不平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B在数轴上分别表示a,b.
(1)对照数轴填写下表:
a | 6 | -6 | -6 | -6 | 2 | -1.5 |
b | 4 | 0 | 4 | -4 | -10 | -1.5 |
A、B两点的距离 |
(2)若A、B两点间的距离记为d,试问:d和a,b有何数量关系?
(3)在数轴上找出所有符合条件的整数点P,使它到5和-5的距离之和为10,并求所有这些整数的和;
(4)若点C表示的数为x,当点C在什么位置时,![]() 取得的值最小? 最小值是多少?
取得的值最小? 最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).
(1)求此抛物线的解析式;
(2)写出顶点坐标及对称轴;
(3)若抛物线上有一点B,且S△OAB=3,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形ABC的直角边AB=6,BC=8,将直角三角形ABC沿边BC的方向平移到三角形DEF的位置,DE交AC于点G,BE=2,三角形CEG的面积为13.5,下列结论:
①三角形ABC平移的距离是4; ②EG=4.5;
③AD∥CF; ④四边形ADFC的面积为6.
其中正确的结论是( )

A. ①② B. ②③ C. ③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是半径为
是半径为 ![]() 的⊙
的⊙ ![]() 的直径,
的直径, ![]() 是圆上异于
是圆上异于 ![]() ,
, ![]() 的任意一点,
的任意一点, ![]() 的平分线交⊙
的平分线交⊙ ![]() 于点
于点 ![]() ,连接
,连接 ![]() 和
和 ![]() ,△
,△ ![]() 的中位线所在的直线与⊙
的中位线所在的直线与⊙ ![]() 相交于点
相交于点 ![]() 、
、 ![]() ,则
,则 ![]() 的长是.
的长是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丫头和爸爸从家出发到大剧院观看“巴交有声”巴蜀中学新年演奏会,爸爸先出发,2分钟后丫头沿同一路线出发去追爸爸,当丫头追上爸爸时发现背包落在途中了,爸爸立即返回找背包,丫头继续前往大剧院,当丫头到达大剧院时,爸爸刚好找到背包并立即前往大剧院![]() 爸爸找背包的时间不计
爸爸找背包的时间不计![]() ,丫头在大剧院等了一会,没有等到爸爸,就沿同一路线返回接爸爸,最终与爸爸会合,丫头和爸爸的速度始终不变,如图是丫头和爸爸两人之间的距离
,丫头在大剧院等了一会,没有等到爸爸,就沿同一路线返回接爸爸,最终与爸爸会合,丫头和爸爸的速度始终不变,如图是丫头和爸爸两人之间的距离![]() 米
米![]() 与丫头出发的时间
与丫头出发的时间![]() 分钟
分钟![]() 的函数图象,则丫头在大剧院等了爸爸______分钟.
的函数图象,则丫头在大剧院等了爸爸______分钟.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com