Question

【题目】如图，ABCD中，AB=2，以点A为圆心，AB为半径的圆交边BC于点E，连接DE、AC、AE．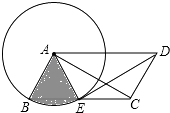

（1）求证：△AED≌△DCA；
（2）若DE平分∠ADC且与⊙A相切于点E，求图中阴影部分（扇形）的面积．

Answer 1

【答案】
（1）证明：∵四边形ABCD是平行四边形，

∴AB=CD，AD∥BC，

∴四边形AECD是梯形，

∵AB=AE，

∴AE=CD，

∴四边形AECD是等腰梯形，

∴AC=DE，

在△AED和△DCA中，

，

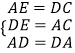∴△AED≌△DCA（SSS）

（2）解：∵DE平分∠ADC，

∴∠ADC=2∠ADE，

∵四边形AECD是等腰梯形，

∴∠DAE=∠ADC=2∠ADE，

∵DE与⊙A相切于点E，

∴AE⊥DE，

即∠AED=90°，

∴∠ADE=30°，

∴∠DAE=60°，

∴∠DCE=∠AEC=180°﹣∠DAE=120°，

∵四边形ABCD是平行四边形，

∴∠BAD=∠DCE=120°，

∴∠BAE=∠BAD﹣∠EAD=60°，

∴S阴影= ×π×22= π．

【解析】（1）利用平行四边形的性质和等腰梯形的判定与性质可证得全等；（2）由切线的性质定理和等腰梯形的性质、平行四边形的性质求出阴影扇形的圆心角度数，进而求出面积.
【考点精析】利用平行四边形的性质和切线的性质定理对题目进行判断即可得到答案，需要熟知平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径．