练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，点D为BC边的中点，点E为AC上一点，将∠C沿DE翻折，使点C落在AB上的点F处，若∠AEF=50°，则∠A的度数为____．

    【答案】65°

    【解析】

    由点D为BC的中点，得BD=CD，根据折叠的性质得到DF=CD，∠EFD=∠C，得DF=BD，根据等腰三角形的性质得∠BFD=∠B，由三角形的内角和与平角的定义得∠A=∠AFE，于是求出∠A的度数.

    ∵点D为BC的中点，

    ∴BD=CD，

    ∵将∠C沿DE翻折，使点C落在AB上的点F处，

    ∴DF=CD，∠EFD=∠C，

    ∴DF=BD，

    ∴∠BFD=∠B，

    ∵∠A=180°-∠C-∠B，∠AFE=180°-∠EFD-∠DFB，

    ∴∠A=∠AFE，

    ∵∠AEF=50°，

    ∴∠A=（180°-50°）=65°.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某海域有A，B，C三艘船正在捕鱼作业，C船突然出现故障，向A，B两船发出紧急求救信号，此时B船位于A船的北偏西72°方向，距A船24海里的海域，C船位于A船的北偏东33°方向，同时又位于B船的北偏东78°方向．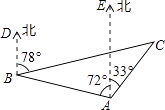

    （1）求∠ABC的度数；
    （2）A船以每小时30海里的速度前去救援，问多长时间能到出事地点．（结果精确到0.01小时）．
    （参考数据： ≈1.414， ≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点 O 在直线 AB 上，OC⊥OD，∠EDO 与∠1 互余．

    (1)求证：ED//AB；

    (2)OF 平分∠COD 交 DE 于点 F，若OFD=70，补全图形，并求∠1 的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C=90°，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多为（　　）

    A. 4 B. 5 C. 6 D. 7

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=5，AC=3，AD，AE分别为△ABC的中线和角平分线，过点C作CH⊥AE于点H，并延长交AB于点F，连结DH，则线段DH的长为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】A，B，C三人玩篮球传球游戏，游戏规则是：第一次传球由A将球随机地传给B，C两人中的某一人，以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人．
    （1）求两次传球后，球恰在B手中的概率；
    （2）求三次传球后，球恰在A手中的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，CA=CB，CD=CE，∠ACB=∠DCE=α．

    （1）求证：BE=AD；

    （2）当α=90°时，取AD，BE的中点分别为点P、Q，连接CP，CQ，PQ，如图②，判断△CPQ的形状，并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，ABCD中，AB=2，以点A为圆心，AB为半径的圆交边BC于点E，连接DE、AC、AE．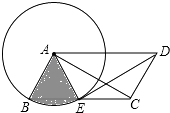

    （1）求证：△AED≌△DCA；
    （2）若DE平分∠ADC且与⊙A相切于点E，求图中阴影部分（扇形）的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一次数学活动中，检验两条纸带①、②的边线是否平行，小明和小丽采用两种不同的方法：小明对纸带①沿AB折叠，量得∠1=∠2=50°；小丽对纸带②沿GH折叠，发现GD与GC重合，HF与HE重合． 则下列判断正确的是（ ）

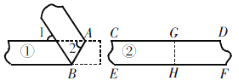
    A. 纸带①的边线平行，纸带②的边线不平行 B. 纸带①、②的边线都平行

    C. 纸带①的边线不平行，纸带②的边线平行 D. 纸带①、②的边线都不平行

    查看答案和解析>>

    同步练习册答案