
【题目】如图1,CA=CB,CD=CE,∠ACB=∠DCE=α.
(1)求证:BE=AD;

(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

【答案】(1)见解析(2)△CPQ为等腰直角三角形,理由见解析
【解析】
(1)易证△ACD≌△BCE,即可求证;
(2)先证明△ACP≌△BCQ,得CP=CQ,∠ACP=∠BCQ,再由∠ACB=90°,得出△PCQ为等腰直角三角形.
(1)如图1,∵∠ACB=∠DCE=α,
∴∠ACD=∠BCE,
又CA=CB,CD=CE,
∴△ACD≌△BCE(SAS)
∴BE=AD;
(2)△CPQ为等腰直角三角形,
证明如图2,由(1)得BE=AD,
∵AD,BE的中点分别为点P、Q,
∴AP=BQ
∵△ACD≌△BCE
∴∠CAP=∠CBQ,
在△ACP和△BCQ中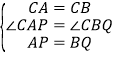
∴△ACP≌△BCQ(SAS)
∴CP=CQ,且∠ACP=∠BCQ
又∵∠ACP+∠PCB=90°,
∴∠BCQ+∠PCB=90°,
∴∠PCQ=90°,
∴△CPQ为等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分∠CAB交CE于点F,DF的延长线交AC于点G,
求证:(1)DF∥BC;
(2)FG=FE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场对今年端午节这天销售A、B、C三种品牌粽子的情况进行了统计,绘制如图1和图2所示的统计图.根据图中信息解答下列问题:

(1)求销售这三种品牌粽子共多少个?
(2)请补全图1中的条形统计图;
(3)求A品牌粽子在图2中所对应的圆心角的度数;
(4)若该商场准备明年端午节期间购进粽子6000个,那应该对A、B、C三种品牌何进货?请你提出一条合理化的建议
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D为BC边的中点,点E为AC上一点,将∠C沿DE翻折,使点C落在AB上的点F处,若∠AEF=50°,则∠A的度数为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料后完成.
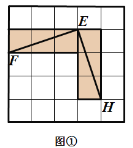
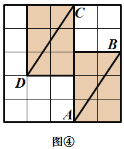
有这样一个游戏,游戏规则如下所述:如图①—图④,都是边 长为![]() 的
的![]() 网格图,其中每条实线称为格线,格线与格线的交 点称为格点.在图①和图②中,可知
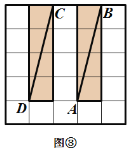
网格图,其中每条实线称为格线,格线与格线的交 点称为格点.在图①和图②中,可知![]() .在图③ 和图④中,可知
.在图③ 和图④中,可知![]() . 根据上面的游戏规则,同学们开始闯关吧! 第一关:在图⑤的
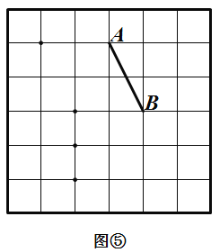
. 根据上面的游戏规则,同学们开始闯关吧! 第一关:在图⑤的![]() 网格图中,所给各点均为格点,经过 给定的一点(不包括边框上的点),在图中画出一条与线段
网格图中,所给各点均为格点,经过 给定的一点(不包括边框上的点),在图中画出一条与线段![]() 垂直 的线段(或者直线)
垂直 的线段(或者直线)![]() ,再画出与线段
,再画出与线段![]() 平行的一条线段(或者 直线)
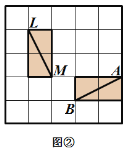
平行的一条线段(或者 直线)![]() . 第二关:在图⑥的
. 第二关:在图⑥的![]() 网格图中,所给各点均为格点,经过 两对给定的点,构造两条互相垂直的直线.(在图中直接画出)
网格图中,所给各点均为格点,经过 两对给定的点,构造两条互相垂直的直线.(在图中直接画出)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() ,点
,点![]() 是直线
是直线![]() 上一个动点(不与
上一个动点(不与![]() 重合),点
重合),点![]() 是
是![]() 边上一个定点, 过点
边上一个定点, 过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() .
.
![]() 如图①,当点
如图①,当点![]() 在线段
在线段![]() 上时,求证:
上时,求证:![]() .
.

![]() 在
在![]() 的条件下,判断
的条件下,判断![]() 这三个角的度数和是否为一个定值? 如果是,求出这个值,如果不是,说明理由.
这三个角的度数和是否为一个定值? 如果是,求出这个值,如果不是,说明理由.
![]() 如图②,当点
如图②,当点![]() 在线段
在线段 ![]() 的延长线上时,(2)中的结论是否仍然成立?如果不成立, 请直接写出
的延长线上时,(2)中的结论是否仍然成立?如果不成立, 请直接写出![]() 之间的关系.
之间的关系.
![]() )当点
)当点![]() 在线段
在线段![]() 的延长线上时,(2)中的结论是否仍然成立?如果不成立,请直接 写出
的延长线上时,(2)中的结论是否仍然成立?如果不成立,请直接 写出![]() 之间的关系.
之间的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习三角形知识时,发现如下三个有趣的结论:在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() 为直线
为直线![]() 上一点,
上一点,![]() ,
,![]() 为垂足,
为垂足,![]() 的平分线交直线
的平分线交直线![]() 于点
于点![]() ,回答下列问题并说明.(可在图上标注数字角)
,回答下列问题并说明.(可在图上标注数字角)
(1)如图①,![]() 为边
为边![]() 上一点,则
上一点,则![]() 、
、![]() 的位置关系是________.请给予证明;
的位置关系是________.请给予证明;

(2)如图②,![]() 为边
为边![]() 反向延长线上一点,则
反向延长线上一点,则![]() 、
、![]() 的位置关系是________.(请直接写出结论)
的位置关系是________.(请直接写出结论)

(3)如图③,![]() 为边
为边![]() 延长线上一点,则
延长线上一点,则![]() 、
、![]() 的位置关系是________.请给予证明.
的位置关系是________.请给予证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com