
【题目】小明在学习三角形知识时,发现如下三个有趣的结论:在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() 为直线
为直线![]() 上一点,
上一点,![]() ,
,![]() 为垂足,
为垂足,![]() 的平分线交直线
的平分线交直线![]() 于点
于点![]() ,回答下列问题并说明.(可在图上标注数字角)
,回答下列问题并说明.(可在图上标注数字角)
(1)如图①,![]() 为边
为边![]() 上一点,则
上一点,则![]() 、
、![]() 的位置关系是________.请给予证明;
的位置关系是________.请给予证明;

(2)如图②,![]() 为边
为边![]() 反向延长线上一点,则
反向延长线上一点,则![]() 、
、![]() 的位置关系是________.(请直接写出结论)
的位置关系是________.(请直接写出结论)

(3)如图③,![]() 为边
为边![]() 延长线上一点,则
延长线上一点,则![]() 、
、![]() 的位置关系是________.请给予证明.
的位置关系是________.请给予证明.

【答案】(1)![]() ,见解析;(2)
,见解析;(2)![]() ;(3)
;(3)![]() ,见解析
,见解析
【解析】
(1)根据∠A=90°,![]() ,得∠CME=∠ABC,再由四边形内角和知∠ABC+∠AME=180°,再由BD平分∠ABC,ME平分∠AME可得
,得∠CME=∠ABC,再由四边形内角和知∠ABC+∠AME=180°,再由BD平分∠ABC,ME平分∠AME可得![]() ,
,![]() ,即得到
,即得到![]() ,
,
(2)由题意可以得到∠AME=∠ABC,又由BD平分∠ABC,ME平分∠AME可以得到∠AMF=∠ABD,即可得到∠AMF+∠ADB=90°即可得到![]() ,
,
(3)先根据题意延长BD交EF于N,根据题意得出∠ABD=∠DMN,再根据三角形内角和即可得出![]() .
.
解:(1)![]()
证明:∵![]() ,
,
∴![]() ;
;
∵在四边形![]() 中,
中,![]() ,
,
∴![]() ;
;
∵![]() 平分
平分![]() ,
,
∴![]() ;
;
同理![]() ,
,
∴![]() ;
;
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)![]()
(3)![]()
证明:延长![]() 交
交![]() 于点
于点![]() ,
,
在![]() 与
与![]() 中
中
![]()
∵![]() 与
与![]() 为对顶角,
为对顶角,
∴![]() ;
;
∵![]() ,
,
∴![]() ;
;
∵![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
在![]() 与
与![]() 中
中
![]() ,
,
∵![]() 与
与![]() 为对顶角,
为对顶角,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,CA=CB,CD=CE,∠ACB=∠DCE=α.
(1)求证:BE=AD;

(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中,x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 |
y | 0 | ﹣3 | ﹣4 | ﹣3 |
下列结论:
①ac<0;
②当x>1时,y随x的增大而增大;
③﹣4是方程ax2+(b﹣4)x+c=0的一个根;
④当﹣1<x<0时,ax2+(b﹣1)x+c+3>0.其中正确结论的个数为( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学活动中,检验两条纸带①、②的边线是否平行,小明和小丽采用两种不同的方法:小明对纸带①沿AB折叠,量得∠1=∠2=50°;小丽对纸带②沿GH折叠,发现GD与GC重合,HF与HE重合. 则下列判断正确的是( )
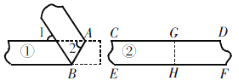
A. 纸带①的边线平行,纸带②的边线不平行 B. 纸带①、②的边线都平行
C. 纸带①的边线不平行,纸带②的边线平行 D. 纸带①、②的边线都不平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法,例如:
①用配方法分解因式:![]() .
.
解:原式![]()
②![]() ,利用配方法求
,利用配方法求![]() 的最小值.
的最小值.
解:![]()
∵![]() ,
,![]()
∴当![]() 时,
时,![]() 有最小值1.
有最小值1.
请根据上述材料解决下列问题:
(1)在横线上添加一个常数,使之成为完全平方式:![]() ________.
________.
(2)用配方法因式分解:![]() .
.
(3)若![]() ,求
,求![]() 的最小值.
的最小值.
(4)已知![]() ,则
,则![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B在数轴上分别表示a,b.
(1)对照数轴填写下表:
a | 6 | -6 | -6 | -6 | 2 | -1.5 |
b | 4 | 0 | 4 | -4 | -10 | -1.5 |
A、B两点的距离 |
(2)若A、B两点间的距离记为d,试问:d和a,b有何数量关系?
(3)在数轴上找出所有符合条件的整数点P,使它到5和-5的距离之和为10,并求所有这些整数的和;
(4)若点C表示的数为x,当点C在什么位置时,![]() 取得的值最小? 最小值是多少?
取得的值最小? 最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).
(1)求此抛物线的解析式;
(2)写出顶点坐标及对称轴;
(3)若抛物线上有一点B,且S△OAB=3,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是半径为
是半径为 ![]() 的⊙
的⊙ ![]() 的直径,
的直径, ![]() 是圆上异于
是圆上异于 ![]() ,
, ![]() 的任意一点,
的任意一点, ![]() 的平分线交⊙
的平分线交⊙ ![]() 于点
于点 ![]() ,连接
,连接 ![]() 和
和 ![]() ,△
,△ ![]() 的中位线所在的直线与⊙
的中位线所在的直线与⊙ ![]() 相交于点
相交于点 ![]() 、
、 ![]() ,则
,则 ![]() 的长是.
的长是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是二元一次方程组的不同解法,请你把下列消元的过程填写完整:
对于二元一次方程组 
(1)方法一:由 ![]() ,得
,得 ![]()
把 ![]() 代入
代入 ![]() ,得________________.
,得________________.
(2)方法二:![]() ,得
,得![]()
![]() ,得________________.
,得________________.
(3)方法三:![]() ,得
,得 ![]()
![]() ,得________________.
,得________________.
(4)方法四:由 ![]() ,得
,得 ![]() ⑥
⑥
把 ![]() 代入⑥,得________________.
代入⑥,得________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com