
����Ŀ����֪A��B�������Ϸֱ��ʾa��b��
(1)��������������
a | 6 | ��6 | ��6 | ��6 | 2 | ��1.5 |
b | 4 | 0 | 4 | ��4 | ��10 | ��1.5 |
A��B����ľ��� |
(2)��A��B�����ľ����Ϊd�����ʣ�d��a��b�к�������ϵ?
(3)���������ҳ����з���������������P��ʹ����5�ͣ�5�ľ���֮��Ϊ10������������Щ�����ĺͣ�
(4)����C��ʾ����Ϊx������C��ʲôλ��ʱ��![]() ȡ�õ�ֵ��С? ��Сֵ�Ƕ��٣�
ȡ�õ�ֵ��С? ��Сֵ�Ƕ��٣�
���𰸡���1��2��6��10��2��12��0����2��![]() ����3��0����4����C��-1��2֮��ʱ��ȡ����СֵΪ3
����3��0����4����C��-1��2֮��ʱ��ȡ����СֵΪ3
��������
��1�����������ϵ����㣬��������뼴�ɣ�
��2�������������ľ��뼴Ϊ��ľ���ֵ��
��3�������������֮�͵���������֮��ľ���ĵ�ļ�����������֮������ߣ����ɵý⣻
��4��![]() ��ʾx��-1�ľ��룬ͬ��
��ʾx��-1�ľ��룬ͬ��![]() ��ʾx��2�ľ��룬���⼰ת��Ϊ������һ�㵽-1��2�ľ������С.
��ʾx��2�ľ��룬���⼰ת��Ϊ������һ�㵽-1��2�ľ������С.
��1�������⣬��
A��B�����ľ�������Ϊ��2��6��10��2��12��0��
��2�������⣬��
![]()
��3�������������֮�͵���������֮��ľ���ĵ�ļ�����������֮�������
��p��һ����5��-5֮��
��������������1,2,3,4,5,-5,-4,-3,-2,-1,0
�����ǵĺ�Ϊ0��
��4�������⣬��
![]() ��ʾx��-1�ľ��룬ͬ��
��ʾx��-1�ľ��룬ͬ��![]() ��ʾx��2�ľ��룬
��ʾx��2�ľ��룬
���C��-1��2֮��ʱ��ȡ����Сֵ����СֵΪ3.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ����
����![]() ��ֱ��
��ֱ��![]() ��һ�����㣨����
��һ�����㣨����![]() �غϣ�����
�غϣ�����![]() ��
��![]() ����һ�����㣬 ����
����һ�����㣬 ����![]() ��
��![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ������
������![]() ������
������![]() ��
��![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ��
��
![]() ��ͼ��������
��ͼ��������![]() ���߶�
���߶�![]() ��ʱ����֤��
��ʱ����֤��![]() ��
��

![]() ��
��![]() �������£��ж�
�������£��ж�![]() �������ǵĶ������Ƿ�Ϊһ����ֵ�� ����ǣ�������ֵ��������ǣ�˵�����ɣ�
�������ǵĶ������Ƿ�Ϊһ����ֵ�� ����ǣ�������ֵ��������ǣ�˵�����ɣ�
![]() ��ͼ��������
��ͼ��������![]() ���߶�
���߶� ![]() ���ӳ�����ʱ����2���еĽ����Ƿ���Ȼ����������������� ��ֱ��д��
���ӳ�����ʱ����2���еĽ����Ƿ���Ȼ����������������� ��ֱ��д��![]() ֮��Ĺ�ϵ��
֮��Ĺ�ϵ��
![]() ������
������![]() ���߶�
���߶�![]() ���ӳ�����ʱ����2���еĽ����Ƿ���Ȼ�������������������ֱ�� д��
���ӳ�����ʱ����2���еĽ����Ƿ���Ȼ�������������������ֱ�� д��![]() ֮��Ĺ�ϵ��
֮��Ĺ�ϵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������8�֣���֪����ͼ����ABC�У�D��AB���е㣬E��AC��һ�㣬EF��AB��DF��BE��
(1)���룺DF��AE�Ĺ�ϵ��______��
(2)��˵����������ȷ�ԣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=a��x��m��2��a��x��m����a��mΪ��������a��0����
��1����֤������a��mΪ��ֵ���ú�����ͼ����x���������������㣻
��2����ú�����ͼ����x�����������ΪA��x1 �� 0����B��x2 �� 0������x12+x22=25����m��ֵ��
��3����ú�����ͼ��Ķ���ΪC����x�ύ��A��B���㣬�ҡ�ABC�����Ϊ1����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧϰ������֪ʶʱ����������������Ȥ�Ľ��ۣ���![]() �У�
��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() Ϊֱ��
Ϊֱ��![]() ��һ�㣬
��һ�㣬![]() ��
��![]() Ϊ���㣬
Ϊ���㣬![]() ��ƽ���߽�ֱ��
��ƽ���߽�ֱ��![]() �ڵ�
�ڵ�![]() ���ش��������Ⲣ˵����������ͼ�ϱ�ע���ֽǣ�
���ش��������Ⲣ˵����������ͼ�ϱ�ע���ֽǣ�
��1����ͼ�٣�![]() Ϊ��
Ϊ��![]() ��һ�㣬��
��һ�㣬��![]() ��
��![]() ��λ�ù�ϵ��________�������֤����
��λ�ù�ϵ��________�������֤����

��2����ͼ�ڣ�![]() Ϊ��
Ϊ��![]() �����ӳ�����һ�㣬��
�����ӳ�����һ�㣬��![]() ��
��![]() ��λ�ù�ϵ��________������ֱ��д�����ۣ�
��λ�ù�ϵ��________������ֱ��д�����ۣ�

��3����ͼ�ۣ�![]() Ϊ��
Ϊ��![]() �ӳ�����һ�㣬��
�ӳ�����һ�㣬��![]() ��
��![]() ��λ�ù�ϵ��________�������֤����
��λ�ù�ϵ��________�������֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������AB1C1D1�ı߳�Ϊ1����B1=60�㣻��AD2��B1C1�ڵ�D2 �� ��AD2Ϊһ�ߣ����ڶ�������AB2C2D2 �� ʹ��B2=60�㣻��AD3��B2C2�ڵ�D3 �� ��AD3Ϊһ��������������AB3C3D3 �� ʹ��B3=60�㡭�������ƣ��������ĵ�n������ABnCnDn�ı�ADn�ij��� �� 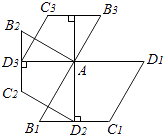
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳����ͼ1��AB��CD����PAB=135������PCD=125�������APC������С����˼·�ǣ���ͼ2����P��PE��AB��ͨ��ƽ�������ʣ�����á�APC�Ķ�������д�����������̣�
����Ǩ�ƣ�
(1)��ͼ3��AD��BC����P������OM���˶�������P��A��B����֮���˶�ʱ����ADP=��������BCP=��������CPD������������֮���к�������ϵ����˵�����ɣ�
(2)��(1)�������£������P��A��B��������˶�ʱ(��P���A��B��O���㲻�غ�)������ֱ��д����CPD���������������������ϵ��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ó�Ϊ ![]() �����Ͻ����Ƴɡ��ա����δ���������Ŀ�Ϊ
�����Ͻ����Ƴɡ��ա����δ���������Ŀ�Ϊ ![]() �������������Ϊ
�������������Ϊ ![]() �����Ͻ����Ŀ��Ȳ��ƣ���
�����Ͻ����Ŀ��Ȳ��ƣ���
������� ![]() ��
�� ![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
������ΰ��Ŵ���ij��Ϳ�������ʹ�ô������������������ʱ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y=��![]() x+8��x�ᡢy��ֱ��ڵ�A�͵�B��M��OB�ϵ�һ�㣬������ABM��AM�۵�����Bǡ������x���ϵĵ�B��������ֱ��AM�ĺ�������ʽ�ǣ�������
x+8��x�ᡢy��ֱ��ڵ�A�͵�B��M��OB�ϵ�һ�㣬������ABM��AM�۵�����Bǡ������x���ϵĵ�B��������ֱ��AM�ĺ�������ʽ�ǣ�������

A. y=��![]() x+8 B. y=��
x+8 B. y=��![]() x+8 C. y=��
x+8 C. y=��![]() x+3 D. y=��
x+3 D. y=��![]() x+3
x+3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com