
����Ŀ����֪��![]() ����
����![]() ��ֱ��
��ֱ��![]() ��һ�����㣨����
��һ�����㣨����![]() �غϣ�����
�غϣ�����![]() ��
��![]() ����һ�����㣬 ����
����һ�����㣬 ����![]() ��
��![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ������
������![]() ������
������![]() ��
��![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ��
��
![]() ��ͼ��������
��ͼ��������![]() ���߶�
���߶�![]() ��ʱ����֤��
��ʱ����֤��![]() ��
��

![]() ��
��![]() �������£��ж�
�������£��ж�![]() �������ǵĶ������Ƿ�Ϊһ����ֵ�� ����ǣ�������ֵ��������ǣ�˵�����ɣ�
�������ǵĶ������Ƿ�Ϊһ����ֵ�� ����ǣ�������ֵ��������ǣ�˵�����ɣ�
![]() ��ͼ��������
��ͼ��������![]() ���߶�
���߶� ![]() ���ӳ�����ʱ����2���еĽ����Ƿ���Ȼ����������������� ��ֱ��д��
���ӳ�����ʱ����2���еĽ����Ƿ���Ȼ����������������� ��ֱ��д��![]() ֮��Ĺ�ϵ��
֮��Ĺ�ϵ��
![]() ������
������![]() ���߶�
���߶�![]() ���ӳ�����ʱ����2���еĽ����Ƿ���Ȼ�������������������ֱ�� д��
���ӳ�����ʱ����2���еĽ����Ƿ���Ȼ�������������������ֱ�� д��![]() ֮��Ĺ�ϵ��
֮��Ĺ�ϵ��

���𰸡���1��֤�������������2��![]() �������ǵĶ�����Ϊһ����ֵ����
�������ǵĶ�����Ϊһ����ֵ����![]() ��֤�������������3����������4������������ȷ����Ϊ����EGF-��DEC+��BFG=180��
��֤�������������3����������4������������ȷ����Ϊ����EGF-��DEC+��BFG=180��
��������
��1����������ֱ��ƽ�У��ڴ�����ȣ��ó�![]() ������ֱ��ƽ�У�ͬλ����ȣ��ó�
������ֱ��ƽ�У�ͬλ����ȣ��ó�![]() ������֤��
������֤��![]() ��
��
��2������![]() ��
��![]() ��BE�ڵ�H������ƽ�������ʶ�����
��BE�ڵ�H������ƽ�������ʶ�����![]() ��
��![]() �����ɵõ��𰸣�
�����ɵõ��𰸣�
��3������![]() ��
��![]() ��BE�ڵ�H���õ�
��BE�ڵ�H���õ�![]() ����Ϊ
����Ϊ![]() ������
������![]() ���õ�
���õ�![]() ��������⣮
��������⣮
��4������![]() ��
��![]() ��BE�ڵ�H���á�DEC=��EGH����Ϊ
��BE�ڵ�H���á�DEC=��EGH����Ϊ![]() ������
������![]() ���Ƶá�HGF+��BFG=180�㣬������⣮
���Ƶá�HGF+��BFG=180�㣬������⣮
��1����![]()
��![]()
��![]()
��![]()
��![]()
��2��![]() �������ǵĶ�����Ϊһ����ֵ����
�������ǵĶ�����Ϊһ����ֵ����![]()
����![]() ��
��![]() ��BE�ڵ�H
��BE�ڵ�H
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
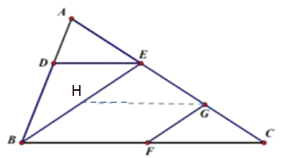
��3������![]() ��
��![]() ��BE�ڵ�H
��BE�ڵ�H
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
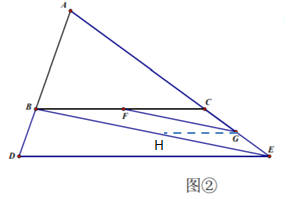
��![]() �Ĺ�ϵ�Գ���
�Ĺ�ϵ�Գ���
��4������![]() ��
��![]() ��BE�ڵ�H
��BE�ڵ�H
���DEC=��EGH
��![]()
��![]()
���HGF+��BFG=180��
�ߡ�HGF=��EGF-��EGH
���HGF=��EGF-��DEC
���EGF-��DEC+��BFG=180��
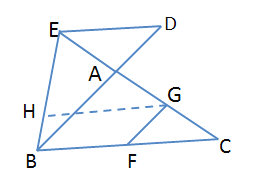
�ࣨ2���еĹ�ϵ����������EGF����DEC����BFG֮���ϵΪ����EGF-��DEC+��BFG=180��
�ʴ�Ϊ������������EGF-��DEC+��BFG=180��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijһ���һ�������Թ�¥Ϊ�������ڶ���������Ӫ������Ϊ����������Ϊ�����г���̣���λ��km�����Ⱥ�����¼���£�![]() .
.
��1�������һ���˿��͵�Ŀ�ĵأ�������¥�������Զ���ڹ�¥��ʲô����
��2����ÿǧ�ļ۸�Ϊ2.4Ԫ��˾��һ�������Ӫҵ���Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90��������ABC��һ��Ϊ�����������Σ�ʹ�����ĵ�������������ABC���������ϣ�����Ի����IJ�ͬ�ĵ��������εĸ������Ϊ��������

A. 4 B. 5 C. 6 D. 7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B��C��������������Ϸ����Ϸ�����ǣ���һ�δ�����A��������ش���B��C�����е�ijһ�ˣ��Ժ��ÿһ�δ��������ϴεĴ���������ش������������е�ijһ�ˣ�
��1�������δ������ǡ��B���еĸ��ʣ�
��2�������δ������ǡ��A���еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��CA=CB��CD=CE����ACB=��DCE=����
��1����֤��BE=AD��

��2������=90��ʱ��ȡAD��BE���е�ֱ�Ϊ��P��Q������CP��CQ��PQ����ͼ�ڣ��ж���CPQ����״��������֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ����Գ���Ϊֱ��x=��1���������н������1��b2��4ac����2��abc��0����3��2a+b=0����4��a+b+c��0����5��a��b+c��0��
����ȷ�Ľ����ǣ� ��
A.��1����2����3����4��
B.��2����4����5��
C.��2����3����4��
D.��1����4����5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�У�AB=2���Ե�AΪԲ�ģ�ABΪ�뾶��Բ����BC�ڵ�E������DE��AC��AE��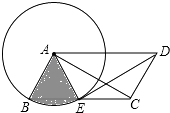
��1����֤����AED�ա�DCA��
��2����DEƽ�֡�ADC�����A�����ڵ�E����ͼ����Ӱ���֣����Σ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���A��20������BE���������ζ��ۣ�����BA����һ�ζ��ۣ���C����BE�ϵ�C��������ʱ��C��DB��74������ԭ�����εġ�C�Ķ���Ϊ�� ��

A.27��B.59��C.69��D.79��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��B�������Ϸֱ��ʾa��b��
(1)��������������
a | 6 | ��6 | ��6 | ��6 | 2 | ��1.5 |
b | 4 | 0 | 4 | ��4 | ��10 | ��1.5 |
A��B����ľ��� |
(2)��A��B�����ľ����Ϊd�����ʣ�d��a��b�к�������ϵ?
(3)���������ҳ����з���������������P��ʹ����5�ͣ�5�ľ���֮��Ϊ10������������Щ�����ĺͣ�
(4)����C��ʾ����Ϊx������C��ʲôλ��ʱ��![]() ȡ�õ�ֵ��С? ��Сֵ�Ƕ��٣�
ȡ�õ�ֵ��С? ��Сֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com