
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,其对称轴为直线x=﹣1,给出下列结果:(1)b2>4ac;(2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.
则正确的结论是( )
A.(1)(2)(3)(4)
B.(2)(4)(5)
C.(2)(3)(4)
D.(1)(4)(5)
【答案】D
【解析】解:(1)如图所示,二次函数与x轴有两个交点,所以b2﹣4ac>0,则b2>4ac.故(1)正确;(2)、(3)如图所示,∵抛物线开口向上,所以a>0,抛物线与y轴交点在负半轴上,
∴c<0.
又﹣ ![]() =﹣1,
=﹣1,
∴b=2a>0,
∴abc<0,2a﹣b<0.
故(2)、(3)错误;(4)如图所示,由图象可知当x=1时,y>0,即a+b+c>0.
故(4)正确;(5)由图象可知当x=﹣1时,y<0,即a﹣b+c<0.
故(5)正确.
综上所述,正确的结论是(1)(4)(5).
所以答案是:D.
【考点精析】解答此题的关键在于理解二次函数图象以及系数a、b、c的关系的相关知识,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,AC=BC=2 ![]() ,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
A.![]() π
π
B.π
C.2 ![]()
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某项工程由甲、乙两队合做12天可以完成,共需工程费用27720元.乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的1.5倍,且甲队每天的工程费用比乙队多250元.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)若工程管理部门决定从这两个队中选一个队单独完成此项工程,从节约资金的角度考虑,应选择哪个工程队?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() ,点
,点![]() 是直线
是直线![]() 上一个动点(不与
上一个动点(不与![]() 重合),点
重合),点![]() 是
是![]() 边上一个定点, 过点
边上一个定点, 过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() .
.
![]() 如图①,当点
如图①,当点![]() 在线段
在线段![]() 上时,求证:
上时,求证:![]() .
.

![]() 在
在![]() 的条件下,判断
的条件下,判断![]() 这三个角的度数和是否为一个定值? 如果是,求出这个值,如果不是,说明理由.
这三个角的度数和是否为一个定值? 如果是,求出这个值,如果不是,说明理由.
![]() 如图②,当点
如图②,当点![]() 在线段
在线段 ![]() 的延长线上时,(2)中的结论是否仍然成立?如果不成立, 请直接写出
的延长线上时,(2)中的结论是否仍然成立?如果不成立, 请直接写出![]() 之间的关系.
之间的关系.
![]() )当点
)当点![]() 在线段
在线段![]() 的延长线上时,(2)中的结论是否仍然成立?如果不成立,请直接 写出
的延长线上时,(2)中的结论是否仍然成立?如果不成立,请直接 写出![]() 之间的关系.
之间的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把抛物线y= ![]() x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= ![]() x2交于点Q,则图中阴影部分的面积为 .
x2交于点Q,则图中阴影部分的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在边CD,BC上,且∠EAF=45°,BD分别交AE,AF于点M,N,以点A为圆心,AB长为半径画弧BD.下列结论:①DE+BF=EF;②BN2+DM2=MN2;③△AMN∽△AFE;④ ![]() 与EF相切;⑤EF∥MN.其中正确结论的个数是( )
与EF相切;⑤EF∥MN.其中正确结论的个数是( )
A.5个
B.4个
C.3个
D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2 , 以AD2为一边,做第二个菱形AB2C2D2 , 使∠B2=60°;作AD3⊥B2C2于点D3 , 以AD3为一边做第三个菱形AB3C3D3 , 使∠B3=60°…依此类推,这样做的第n个菱形ABnCnDn的边ADn的长是 . 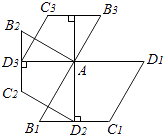
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com