
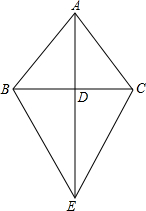
 如图,△ABC中,AB=AC,AD⊥BD于点D,E是AD延长线上的一点,且BC=BE,请判断△BCE的形状,并证明你的结论.
如图,△ABC中,AB=AC,AD⊥BD于点D,E是AD延长线上的一点,且BC=BE,请判断△BCE的形状,并证明你的结论.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 第一次模拟考试后,数学老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到后第二、三、四组的频数比为3:10:8,然后请学生(也请你一起)结合统计图完成下列问题:
第一次模拟考试后,数学老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到后第二、三、四组的频数比为3:10:8,然后请学生(也请你一起)结合统计图完成下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
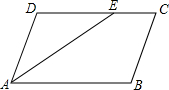 如图,已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD,AB于E,F.
如图,已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD,AB于E,F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com