
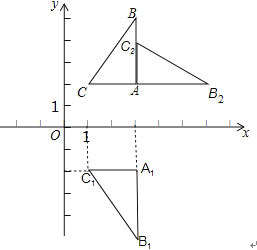
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(3,2)、B(3,5)、C(1,2).
(1)在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;
(2)把△ABC绕点A顺时针旋转一定的角度,得图中的△AB2C2 , 点C2在AB上.
①旋转角为多少度?
②写出点B2的坐标.
【答案】
(1)
解:A(3,2)、B(3,5)、C(1,2)关于x轴的对称点分别为A1(3,﹣2),B1(3,﹣5),C1(1,﹣2),
如图所示,
(2)
解:
①∵A(3,2)、B(3,5)、C(1,2),
∴AB=3,AC=2,BC=![]() ,
,
∵![]() ,
,![]()
∴AB2+AC2=BC2,
∴∠CAB=90°,
∵AC与AC2的夹角为∠CAC2,
∴旋转角为90°;
②∵AB=AB2=3,
∴CB2=AC+AB2=5,
∴B2的坐标为(6,2).
【解析】(1)分别得到点A、B、C关于x轴的对称点,连接点A1 , B1 , C1 , 即可解答;
(2)①根据点A,B,C的坐标分别求出AC,BC,AC的长度,根据勾股定理逆定理得到∠CAB=90°,即可得到旋转角;
②根据旋转的性质可知AB=AB2=3,所以CB2=AC+AB2=5,所以B2的坐标为(6,2).
【考点精析】根据题目的已知条件,利用作轴对称图形的相关知识可以得到问题的答案,需要掌握画对称轴图形的方法:①标出关键点②数方格,标出对称点③依次连线.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上
(1)求斜坡AB的水平宽度BC。
(2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高。(![]() ≈2.236,结果精确到0.1m)
≈2.236,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年益阳市的地区生产总值(第一、二、三产业的增加值之和)已进入千亿元俱乐部,如图表示2014年益阳市第一、二、三产业增加值的部分情况,请根据图中提供的信息解答下列问题
(1)2014年益阳市的地区生产总值为多少亿元?
(2)请将条形统计图中第二产业部分补充完整;
(3)求扇形统计图中第二产业对应的扇形的圆心角度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
(1)试探究AP与BQ的数量关系,并证明你的结论
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.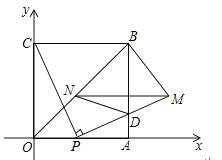
(1)求点M的坐标(用含t的代数式表示);
(2)试判断线段MN的长度是否随点P的位置的变化而改变?并说明理由.
(3)当t为何值时,四边形BNDM的面积最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,曲线y1抛物线的一部分,且表达式为:y1=![]() (x2﹣2x﹣3)(x≤3)曲线y2与曲线y1关于直线x=3对称.
(x2﹣2x﹣3)(x≤3)曲线y2与曲线y1关于直线x=3对称.
(1)求A、B、C三点的坐标和曲线y2的表达式;
(2)过点D作CD∥x轴交曲线y1于点D,连接AD,在曲线y2上有一点M,使得四边形ACDM为筝形(如果一个四边形的一条对角线被另一条对角线垂直平分,这样的四边形为筝形),请求出点M的横坐标;
(3)设直线CM与x轴交于点N,试问在线段MN下方的曲线y2上是否存在一点P,使△PMN的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条公路的转弯处是一段圆弧![]()

(1)用直尺和圆规作出![]() 所在圆的圆心O;(要求保留作图痕迹,不写作法)
所在圆的圆心O;(要求保留作图痕迹,不写作法)
(2)若![]() 的中点C到弦AB的距离为20m,AB=80m,求
的中点C到弦AB的距离为20m,AB=80m,求![]() 所在圆的半径.
所在圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD. 
(1)由AB,BD, ![]() 围成的曲边三角形的面积是;
围成的曲边三角形的面积是;
(2)求证:DE是⊙O的切线;
(3)求线段DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com