
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 ①根据二次函数的性质即可得出抛物线y=6x2的对称轴为y轴,结合a=6>0即可得出当x>0时,y随x的增大而增大,结论①正确;
②将x=-2和1代入一元二次方程可得出x+m的值,再令x+m+2=该数值可求出x值,从而得出结论②正确;
③由“当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0”可得出当x=1时y=0且抛物线的对称轴≥2,解不等式即可得出b≤-4、c≥3,结论③正确.综上即可得出结论.
解答 解:①∵在二次函数y=6x2中,a=6>0,b=0,
∴抛物线的对称轴为y轴,当x>0时,y随x的增大而增大,
∴①结论正确;
②∵关于x的方程a(x+m)2+b=0的解是x1=-2,x2=1,
∴x+m=-2+m或1+m,
∴方程a(x+m+2)2+b=0中,
x+m+2=-2+m或x+m+2=1+m,
解得:x1=-4,x2=-1,
∴②结论正确;
③∵二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,
∴$\left\{\begin{array}{l}{1+b+c=0}\\{-\frac{b}{2}≥2}\end{array}\right.$,
解得:b≤-4,c≥3,
∴结论③正确.
故选D.
点评 本题考查了二次函数的性质、一元二次方程的解以及二次函数的图象,逐一分析三条结论的正误是解题的关键.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:选择题
 如图,已知正方形ABCD的边长为4,点E、F分别在边AB、ABC上,且AE=BF=1,CE、DF相交于点O,下列结论:
如图,已知正方形ABCD的边长为4,点E、F分别在边AB、ABC上,且AE=BF=1,CE、DF相交于点O,下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,O为AC中点,EF过点O且EF⊥AC分别交DC于点F,交AB于点E,点G是AE中点且∠AOG=30°,给出以下结论:
如图,在矩形ABCD中,O为AC中点,EF过点O且EF⊥AC分别交DC于点F,交AB于点E,点G是AE中点且∠AOG=30°,给出以下结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,⊙M与x轴相交于A(2,0)、B(8,0),与y轴相切于点C,P是优弧AB上的一点,则tan∠APB为( )
如图,⊙M与x轴相交于A(2,0)、B(8,0),与y轴相切于点C,P是优弧AB上的一点,则tan∠APB为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
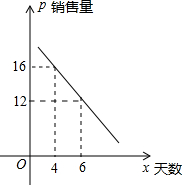 某水果店新进一种水果,进价为20元/盒,为了摸清行情,决定试营销10天,商家通过这10天的市场调查发现:
某水果店新进一种水果,进价为20元/盒,为了摸清行情,决定试营销10天,商家通过这10天的市场调查发现:| 天数 | 1≤x≤5 | 6≤x≤10 |
| 销售价格y | $\frac{1}{2}$x+24 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{64}$的算术平方根是$\frac{1}{8}$ | B. | -3是9的一个平方根 | ||
| C. | 13是(-13)2的算术平方根 | D. | 0.4的算术平方根是0.02 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com