
【题目】如图,A是以BC为直径的⊙O上的一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,点F是EB的中点,连结CF交AD于点G
(1)求证:AF是⊙O的切线;
(2)求证:AG=GD;
(3)若FB=FG,且⊙O的半径长为3![]() ,求BD.
,求BD.
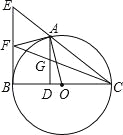
【答案】(1)、证明过程见解析;(2)、证明过程见解析;(3)、2![]()
【解析】
试题分析:(1)、要证AF是⊙O的切线,就是要证明∠FAO=90°,连接AB,根据BE是⊙O的切线和直角三角形的等量代换,就可得出结论;(2)、根据切线判定知道EB⊥BC,而AD⊥BC,从而可以确定AD∥BE,那么△BFC∽△DGC,又点F是EB的中点,就可得出结论;(3)、点F作FH⊥AD于点H,根据前两问的结论,利用三角形的相似性和勾股定理,可以求出BD的长度.
试题解析:(1)、连结AB, ∵BC是⊙O的直径, ∴∠BAC=90°. ∵F是斜边BE的中点,
∴AF=FB=EF, ∴∠FBA=∠FAB, 又∵OA=OB, ∴∠ABO=∠BAO ∵BE是⊙O的切线,
∴∠EBO=90° ∵∠EBO=∠FBA+∠ABO=∠FAB+∠BAO=∠FAO=90° ∴AF是⊙O的切线;
(2)、∵BC是⊙O的直径,BE是⊙O的切线, ∴EB⊥BC. 又∵AD⊥BC, ∴AD∥BE,
∴△BFC∽△DGC,△FEC∽△GAC, ∴![]() =
=![]() ,
,![]() =
=![]() , ∴
, ∴![]() =
=![]() ,
,
∵F是斜边BE的中点, ∴BF=EF, ∴DG=AG;
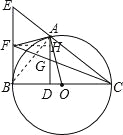
(3)、解:过点F作FH⊥AD于点H, ∵BD⊥AD,FH⊥AD, ∴FH∥BC.由(2),知∠FBA=∠BAF, ∴BF=AF. 由已知,有BF=FG, ∴AF=FG,即△AFG是等腰三角形. ∵FH⊥AD,
∴AH=GH, ∵DG=AG, ∴DG=2HG, 即![]() =
=![]() , ∵FH∥BD,BF∥AD,∠FBD=90°,
, ∵FH∥BD,BF∥AD,∠FBD=90°,
∴四边形BDHF是矩形,BD=FH, ∵FH∥BC,易证△HFG∽△DCG, ∴![]() =
=![]() =
=![]() ,
,
即![]() =
=![]() =
=![]() =
=![]() .
.![]() , ∴BC=6
, ∴BC=6![]() .
.
∴![]() =
=![]() =
=![]() , 解得BD=2
, 解得BD=2![]() . ∴BD=FH=2
. ∴BD=FH=2![]() .
.


科目:初中数学 来源: 题型:
【题目】“六一”期间,某商店将单价标为130元的书包按8折出售可获利30%,该书包每个的进价是( )
A. 65元 B. 80元 C. 100元 D. 104元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )
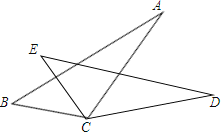
A.AB=DE B.∠B=∠E C.AC=DC D.∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】7+(-3)+(-4)+18+(-11)=(7+18)+[(-3)+(-4)+(-11)]是应用了( )。
A.加法交换律
B.加法结合律
C.分配律
D.加法交换律与加法结合律
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮在上午8时,9时30分,10时,12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年上半年北京市实现地区生产总值15212.5亿元,同比增长6.3%.总体来看,经济保持平稳运行,高质量发展.将数据15212.5用科学记数法表示应为( )
A.1.52125×105B.1.52125×104
C.0.152125×105D.0.152125×106
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com