
【题目】![]() 问题发现
问题发现
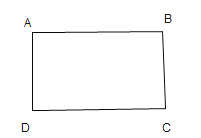
如图![]() ,正方形
,正方形![]() 将正方形
将正方形![]() 绕点
绕点![]() 旋转,直线
旋转,直线![]() 交于点
交于点![]() 请直接写出线段
请直接写出线段![]() 与
与![]() 的数量关系是 ,位置关系是 _;
的数量关系是 ,位置关系是 _;
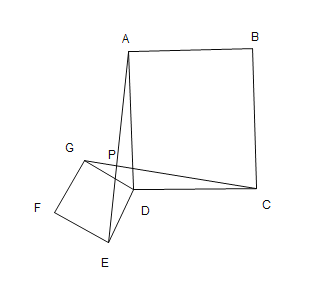
![]() 拓展探究
拓展探究
如图![]() ,矩形
,矩形![]() 将矩形
将矩形![]() 绕点
绕点![]() 旋转,直线
旋转,直线![]() 交于点
交于点![]()
![]() 中线段关系还成立吗/若成立,请写出理由;若不成立,请写出线段
中线段关系还成立吗/若成立,请写出理由;若不成立,请写出线段![]() 的数量关系和位置关系,并说明理由;
的数量关系和位置关系,并说明理由;
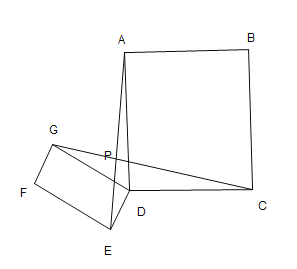
![]() 解决问题
解决问题
在![]() 的条件下,
的条件下,![]() 矩形
矩形![]() 绕
绕![]() 点旋转过程中,请直接写出当点
点旋转过程中,请直接写出当点![]() 与点
与点![]() 重合时,线段
重合时,线段![]() 的长,
的长,
【答案】![]() ;
;![]() 中数量关系不成立,位置关系成立.
中数量关系不成立,位置关系成立.![]() ,理由见解析;
,理由见解析;![]() 或
或![]()
【解析】
(1)证明△ADE≌△CDG(SAS),可得AE=CG,∠DAG=∠DCG,再由直角三角形两个锐角互余即可证得AE⊥CG;
(2)先证明△ADE∽△CDG,利用相似三角形的性质证明即可.
(3)先通过作图找到符合题意的两种情况,第一种情况利用勾股定理求解即可;第二种情况借助相似三角形及勾股定理计算即可.
(1)![]() ;
;
理由如下:由题意知在正方形![]() 中,
中,
![]() ,
,![]() ,
,
![]()
![]()
在△ADE与△CDG中,
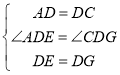
∴△ADE≌△CDG(SAS)
∴![]() ,
,![]()
∵对顶角相等,
∴![]()
![]()
![]() .
.
(2)(1)中数量关系不成立,位置关系成立.即:![]()
理由如下:
由题意知在矩形![]() 中,
中,![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,![]()
∵对顶角相等
∴![]()
![]()
![]() .
.
综上所述:![]()
(3)
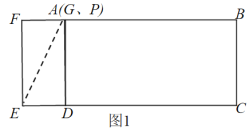
如图1,当点G、P在点A处重合时,连接AE,
则此时∠ADE=∠GDE=90°
∴在Rt△ADE中,AE=![]() ,
,
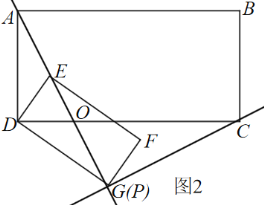
如图1,当点G、P重合时, 则点A、E、G在同一直线上,
∵AD=DG=4,
∴∠DAG=∠DGA,
∵∠ADC=∠AGP=90°,∠AOD=∠COG,
∴∠DAG=∠COG,
∴∠DGA=∠COG,
又∵∠GDO=∠CDG,
∴△GDO∽△CDG,
∴![]()
∴![]()
∴DO=2,CG=2OG,
∴OC=DC-DO=8-2=6,
∵在Rt△COG中,OG2+GC2=OC2,
∴OG2+(2OG)2=62,
∴OG=![]() (舍负),
(舍负),
∴CG=![]() ,
,
由(2)得:![]()
∴AE=![]() ,
,
综上所述,AE的长为![]() 或
或![]() .
.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
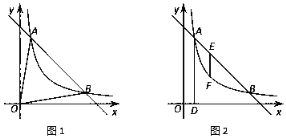
【题目】如图1,点A(m,6),B(6,1)在反比例函数图象上,作直线AB,连接OA、OB.
(1)求反比例函数的表达式和m的值;
(2)求△AOB的面积;
(3)如图2,E是线段AB上一点,作AD⊥x轴于点D,过点E作x轴的垂线,交反比例函数图象于点F,若EF=![]() AD,求出点E的坐标.
AD,求出点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 有两个不同的交点.下列结论:①
有两个不同的交点.下列结论:①![]() ;②当
;②当![]() 时,
时,![]() 有最小值
有最小值![]() ;③方程
;③方程![]() 有两个不等实根;④若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,则
有两个不等实根;④若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,则![]() ;其中正确的结论的个数是( )
;其中正确的结论的个数是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年中国北京世界园艺博览会已于2019年4月29日在北京市延庆区开展,吸引了大批游客参观游览.五一小长假期间平均每天入园人数大约是8万人,佳佳等5名同学组成的学习小组,随机调查了五一假期中入园参观的部分游客,获得了他们在园内参观所用时间,并对数据进行整理,描述和分析,下面给出了部分信息:
a.参观时间的频数分布表如下:
时间 | 频数(人数) | 频率 |
| 25 | 0.050 |
| 85 |
|
| 160 | 0.320 |
| 139 | 0.278 |
|
| 0.100 |
| 41 | 0.082 |
合计 |
| 1.000 |
b.参观时间的频数分布直方图如图:
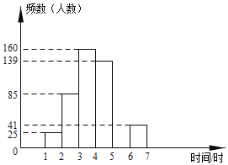
根据以上图表提供的信息,解答下列问题:
(1)这里采用的调查方式是 ;
(2)表中![]() ,
,![]() ,
,![]() ;
;
(3)并请补全频数分布直方图;
(4)请你估算五一假期中平均每天参观时间小于4小时的游客约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点![]() 和
和![]() 是一次函数
是一次函数![]() 与反比例函数
与反比例函数![]() 图象的两个不同交点,点
图象的两个不同交点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 以及
以及![]() 分别与
分别与![]() 轴交与点
轴交与点![]() 和点
和点![]() .
.
(1)求反比例函数![]() 的表达式;
的表达式;
(2)若![]() ,求
,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠BAC.
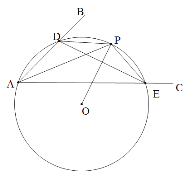
(1)如图,在平面内任取一点O;
(2)以点O为圆心,OA为半径作圆,交射线AB于点D,交射线AC于点E;
(3)连接DE,过点O作线段DE的垂线交⊙O于点P;
(4)连接AP,DP和PE.根据以上作图过程及所作图形,下列四个结论中:
①△ADE是⊙O的内接三角形; ② ![]() ;
;
③ DE=2PE; ④ AP平分∠BAC.
所有正确结论的序号是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平而直角坐标系![]() 中,函数
中,函数![]() (其中
(其中![]() ,
,![]() )的图象经过平行四边形
)的图象经过平行四边形![]() 的顶点
的顶点![]() ,函数
,函数![]() (其中
(其中![]() )的图象经过顶点
)的图象经过顶点![]() ,点
,点![]() 在
在![]() 轴上,若点
轴上,若点![]() 的横坐标为1,
的横坐标为1,![]() 的面积为
的面积为![]() .
.
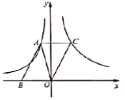
(1)求![]() 的值:
的值:
(2)求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,二次函数![]() 与一次函数
与一次函数![]() (a,b为常数,且
(a,b为常数,且![]() ).
).
(1)若y1,y2的图象都经过点(2,3),求y1,y2的表达式;
(2)当y2经过点![]() 时,y1也过A,B两点:
时,y1也过A,B两点:
①求m的值;
②![]() 分别在y1,y2的图象上,实数t使得“当
分别在y1,y2的图象上,实数t使得“当![]() 或
或![]() 时,
时,![]() ”,试求t的最小值.
”,试求t的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com