Question

14．已知平面直角坐标系xOy，反比例函数$y=\frac{60}{x}$的图象上有一点B，其横坐标为15，点C在y轴上，若BC=17，则点C的坐标为（0，12）或（0，-4）．

Answer 1

分析 首先根据题意画出图形，然后过点B作BE⊥y轴于点E，作BD⊥x轴于点D，由反比例函数y=$\frac{60}{x}$的图象上有一点B，其横坐标为15，可求得BD，BE的长，利用勾股定理，可求得CE的长，继而求得答案．

解答 解：如图，过点B作BE⊥y轴于点E，作BD⊥x轴于点D，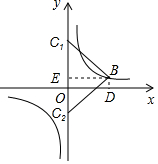

∵反比例函数y=$\frac{60}{x}$的图象上有一点B，其横坐标为15，
∴点B的坐标为：（15，4），
∴BE=15，BD=4，
∵BC=17，
∴EC=$\sqrt{B{C}^{2}-B{E}^{2}}$=8，
∴OC₁=4+8=12，OC₂=8-4=4，
∴点C的坐标为：（0，12）或（0，-4）．
故答案为：（0，12）或（0，-4）．

点评 此题考查了反比例函数图象上点的坐标特征以及勾股定理．注意根据题意画出图形，结合图形求解是关键．