
【题目】在△ABC中,AB=AC=5,cos∠ABC=![]() ,将△ABC绕点C顺时针旋转,得到△A1B1C.
,将△ABC绕点C顺时针旋转,得到△A1B1C.
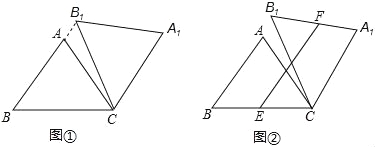
(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1,求线段EF1长度的最大值与最小值的差.
【答案】(1)①见试题解析;②![]() (3)
(3)![]() .
.
【解析】
试题分析:(1)①根据旋转的性质和平行线的性质证明;
②过A作AF⊥BC于F,过C作CE⊥AB于E,根据三角函数和三角形的面积公式解答;
(2)过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,和以C为圆心BC为半径画圆交BC的延长线于F1,得出最大和最小值解答即可.
试题解析:(1)①证明:∵AB=AC,B1C=BC,∴∠AB1C=∠B,∠B=∠ACB,
∵∠AB1C=∠ACB(旋转角相等),∴∠B1CA1=∠AB1C,∴BB1∥CA1;
②过A作AF⊥BC于F,过C作CE⊥AB于E,如图①:
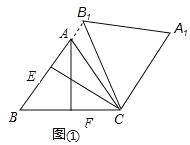
∵AB=AC,AF⊥BC,∴BF=CF,∵cos∠ABC=![]() ,AB=5,∴BF=3,∴BC=6,
,AB=5,∴BF=3,∴BC=6,
∴B1C=BC=6,∵CE⊥AB,∴BE=B1E=![]() ×6=
×6=![]() ,
,
∴BB1=![]() ,CE=
,CE=![]() ×6=
×6=![]() ,∴AB1=
,∴AB1=![]() -5=
-5=![]() ,
,
∴△AB1C的面积为:![]() ;
;
(2)如图2,过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,EF1有最小值,
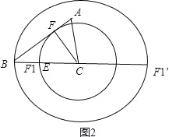
此时在Rt△BFC中,CF=![]() ,∴CF1=
,∴CF1=![]() ,
,
∴EF1的最小值为![]() -3=
-3=![]() ;
;
如图,以C为圆心BC为半径画圆交BC的延长线于F1,EF1有最大值;
此时EF1=EC+CF1=3+6=9,
∴线段EF1的最大值与最小值的差为9-![]() =
=![]() .
.


科目:初中数学 来源: 题型:
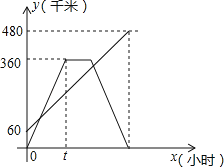
【题目】甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
(1)乙车的速度是 千米/时,t= 小时;
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;
(3)直接写出乙车出发多长时间两车相距120千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
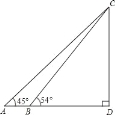
【题目】天塔是天津市的标志性建筑之一,某校数学兴趣小组要测量天塔的高度,如图,他们在点A处测得天塔最高点C的仰角为45°,再往天塔方向前进至点B处测得最高点C的仰角为54°,AB=112m,根据这个兴趣小组测得的数据,计算天塔的高度CD(tan36°≈0.73,结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作为世界文化遗产的长城,其总长大约为6700000m.将6700000用科学记数法表示为( )
A. 6.7×105 B. 6.7×106 C. 0.67×107 D. 67×108
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com