
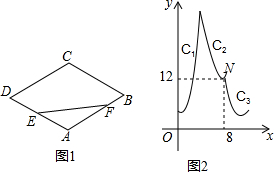
 如图1,在菱形ABCD中,点E为AD的中点,点F为折线A-B-C-D上一个动点(从点A出发到点D停止),连结EF,设点F的运动路径的长为x,EF2为y,y关于x的函数图象由C1,C2,C3三段组成,已知C2与C3的界点N的坐标如图2所示.
如图1,在菱形ABCD中,点E为AD的中点,点F为折线A-B-C-D上一个动点(从点A出发到点D停止),连结EF,设点F的运动路径的长为x,EF2为y,y关于x的函数图象由C1,C2,C3三段组成,已知C2与C3的界点N的坐标如图2所示.分析 (1)N是C2与C3的界点,且四边形ABCD是菱形,此刻点F恰好运动到点C,由此即可解决问题;
(2)由(1)结合图象可知,当点F运动到点C时,在△CDE中,可得DE2+EF2=CD2,推出△CDE是直角三角形,由CD=2DE,可得∠DCE=30°,∠D=60°,如图所示,当F在CD上时(8≤x≤12),作EG⊥CD于G,利用勾股定理即可解决问题;
(3)求出C1,C2,C3段的好像解析式,分情形列出方程,解方程即可解决问题.
解答 解:(1)∵N是C2与C3的界点,且四边形ABCD是菱形,
∴此刻点F恰好运动到点C,
∴菱形的边长=$\frac{8}{2}$=4.
(2)由(1)结合图象可知,当点F运动到点C时,
在△CDE中,∵EF2=12,ED2=4,CD2=16,
∴DE2+EF2=CD2,
∴△CDE是直角三角形,
∵CD=2DE,
∴∠DCE=30°,∠D=60°,
如图所示,当F在CD上时(8≤x≤12),
作EG⊥CD于G,∵∠D=60°,DE=2,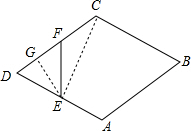
∴DG=1,EG=$\sqrt{3}$,
在Rt△GEF中,GF2+GE2=EF2,
∴y=(11-x)2+3,
∴图象C3段的函数解析式为y=x2-22x+124(8≤x≤12).
(3)同理可得图象C1段的函数解析式为y=x2+2x+4(0≤x≤4),
图象C2段的函数解析式为y=x2-16x+76(4≤x≤8),
图象C3段的函数解析式为y=x2-22x+124(8≤x≤12).
分情形讨论:
当y=7时,7=x2+2x+4,解得x=1或-3(舍弃),
7=x2-16x+76,方程无解,
7=x2-22x+124,解得x=9或13(舍弃),
当y=28时,28=x2+2x+4,解得x=4或-6(舍弃),
28=x2-16x+76,解得x=4或12(舍弃)
28=x2-22x+124,方程在8≤x≤12内无解,
于是当y=28时,x=4,这点刚好是图象C1,C2的解得,也是菱形中的点B,
∴当7≤y≤28时,x的取值范围是1≤x≤9.
点评 本题考查四边形综合题、勾股定理的逆定理、一元二次方程、二次函数等知识,解题的关键是读懂图象信息解决问题,学会用分类讨论的思想实际问题,体现了数形结合的思想,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b=0;②a+c>b;③抛物线y=ax2+bx+c与x轴的另一个交点为(3,0);④abc>0.其中正确的结论是①④(填写序号)
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b=0;②a+c>b;③抛物线y=ax2+bx+c与x轴的另一个交点为(3,0);④abc>0.其中正确的结论是①④(填写序号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
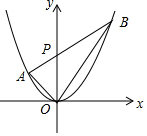 若三角形的一边和该边上的高相等的三角形称为“和谐三角形”,如图,已知抛物线y=ax2经过A(-1,1),P是y轴正半轴上的动点,射线AP与抛物线交于另一点B,当△AOP是“和谐三角形”时,点B的坐标为(2,4)和(1,1).
若三角形的一边和该边上的高相等的三角形称为“和谐三角形”,如图,已知抛物线y=ax2经过A(-1,1),P是y轴正半轴上的动点,射线AP与抛物线交于另一点B,当△AOP是“和谐三角形”时,点B的坐标为(2,4)和(1,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
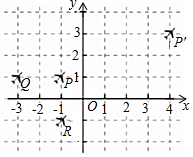 如图所示,三架飞机P,Q,R保持编队飞行,某时刻在坐标系中的坐标分别为(-1,1),(-3,1),(-1,-1).30秒后,飞机P飞到P′(4,3)位置,则飞机Q,R的位置Q′,R′分别为( )
如图所示,三架飞机P,Q,R保持编队飞行,某时刻在坐标系中的坐标分别为(-1,1),(-3,1),(-1,-1).30秒后,飞机P飞到P′(4,3)位置,则飞机Q,R的位置Q′,R′分别为( )| A. | Q′(2,3),R′(4,1) | B. | Q′(2,3),R′(2,1) | C. | Q′(2,2),R′(4,1) | D. | Q′(3,3),R′(3,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
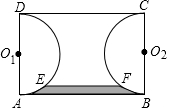 如图,已知矩形ABCD中,AB=3,AD=2,分别以边AD,BC为直径在矩形ABCD的内部作半圆O1和半圆O2,一平行于AB的直线EF与这两个半圆分别交于点E、点F,且EF=2(EF与AB在圆心O1和O2的同侧),则由$\widehat{AE}$,EF,$\widehat{FB}$,AB所围成图形(图中阴影部分)的面积等于3-$\frac{5\sqrt{3}}{4}$-$\frac{π}{6}$.
如图,已知矩形ABCD中,AB=3,AD=2,分别以边AD,BC为直径在矩形ABCD的内部作半圆O1和半圆O2,一平行于AB的直线EF与这两个半圆分别交于点E、点F,且EF=2(EF与AB在圆心O1和O2的同侧),则由$\widehat{AE}$,EF,$\widehat{FB}$,AB所围成图形(图中阴影部分)的面积等于3-$\frac{5\sqrt{3}}{4}$-$\frac{π}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com