
 如图,△ABC的内切圆O与各边分别相切于点D,E,F,那么下列叙述错误的是( )
如图,△ABC的内切圆O与各边分别相切于点D,E,F,那么下列叙述错误的是( )| A. | 点O是△ABC的三条角平分线的交点 | |
| B. | 点O是△DEF的三条中线的交点 | |
| C. | 点O是△DEF的三条边的垂直平分线的交点 | |
| D. | △DEF一定是锐角三角形 |
分析 根据切线的性质得到OD⊥AB,OE⊥BC,OF⊥AC,根据同圆的半径相等得到OD=OE=OF,于是得到点O是△ABC的三条角平分线的交点,根据外接圆的圆心的性质得到点O是△DEF的三条边的垂直平分线的交点,根据四边形的内角和和圆周角定理得到DEF是锐角三角形.
解答 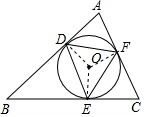 解:连接OD,OE,OF,
解:连接OD,OE,OF,
∵△ABC的内切圆O与各边分别相切于点D,E,F,
∴OD⊥AB,OE⊥BC,OF⊥AC,
∵OD=OE=OF,
∴点O是△ABC的三条角平分线的交点,
∵⊙O是△DEF的外接圆,
∴点O是△DEF的三条边的垂直平分线的交点,
∵∠ADO=∠AFO=90°,
∴∠A+∠DOF=180°,
∴∠DOF=180°-∠A,
∴∠DEF=$\frac{1}{2}$∠DOF=90°-$\frac{1}{2}∠$A,
∴∠DEF是锐角,同理∠EDF与∠DFE是锐角,
∴△DEF是锐角三角形,
故选B.
点评 此题主要考查了三角形的内心与外心的性质;三角形的内心:三条角平分线的交点,到三角形三边的距离相等;三角形的外心:三边中垂线的交点,到三角形三个顶点的距离相等.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
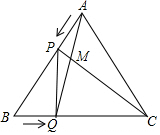 如图,边长为4cm的等边△ABC中,点P、Q分别是边AB、BC上的动点(端点除外),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ,CP交于点M,在点P,Q运动的过程中.
如图,边长为4cm的等边△ABC中,点P、Q分别是边AB、BC上的动点(端点除外),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ,CP交于点M,在点P,Q运动的过程中.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 3 | C. | -3 | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+2)(x-2)=x2-4 | B. | x2-4=(x+2)(x-2) | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | x2+4x-2=x(x+4)-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com