
【题目】如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF 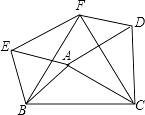
(1)求证:△EBF≌△DFC;
(2)求证:四边形AEFD是平行四边形;
(3)①△ABC满足时,四边形AEFD是菱形.(无需证明) ②△ABC满足时,四边形AEFD是矩形.(无需证明)
③△ABC满足时,四边形AEFD是正方形.(无需证明)
【答案】
(1)证明:∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°,
∴∠ABE﹣∠ABF=∠FBC﹣∠ABF,即∠CBA=∠FBE,
在△ABC和△EBF中,
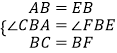 ,
,
∴△ABC≌△EBF(SAS),
∴EF=AC,
又∵△ADC为等边三角形,
∴CD=AD=AC,
∴EF=AD=DC,
同理可得△ABC≌△DFC,
∴DF=AB=AE=DF,
∴四边形AEFD是平行四边形;
∴∠FEA=∠ADF,
∴∠FEA+∠AEB=∠ADF+∠ADC,即∠FEB=∠CDF,
在△FEB和△CDF中,
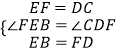 .
.
∴△EBF≌△DFC(SAS)
(2)证明:∵△EBF≌△DFC,
∴EB=DF,EF=DC.
∵△ACD和△ABE为等边三角形,
∴AD=DC,AE=BE,
∴AD=EF,AE=DF
∴四边形AEFD是平行四边形
(3)AB=AC;∠BAC=150°;AB=AC,∠BAC=150°
【解析】(3)①若AB=AC,则平行四边形AEFD是菱形; 此时AE=AB=AC=AD,即△ABC是等腰三角形;
故△ABC满足AB=AC时,四边形AEFD是菱形;
②若∠BAC=150°,则平行四边形AEFD是矩形;
由(1)知四边形AEFD是平行四边形,则∠EAD=90°时,可得平行四边形AEFD是矩形,
∴∠BAC=360°﹣60°﹣60°﹣90°=150°,
即△ABC满足∠BAC=150°时,四边形AEFD是矩形;
③综合①②的结论知:当△ABC是顶角∠BAC是150°的等腰三角形时,四边形AEFD是正方形.
故答案是:①AB=AC;
②∠BAC=150°;
③AB=AC,∠BAC=150°.
(1)由△ABE与△BCF都为等边三角形,利用等边三角形的性质得到两对边相等,∠ABE=∠CBF=60°,利用等式的性质得到夹角相等,利用SAS得到△EBF与△DFC全等;(2)利用(1)中全等三角形对应边相等得到EF=AC,再由三角形ADC为等边三角形得到三边相等,等量代换得到EF=AD,AE=DF,利用对边相等的四边形为平行四边形得到AEFD为平行四边形;(3)①当AE=AD时,ADFE是菱形;②当∠BAC=150°,由此可求得∠EAD的度数,则可得ADFE是矩形;③当ADFE是正方形时,∠EAD=90°,且AE=AD,联立①②的结论即可.
【考点精析】通过灵活运用等边三角形的性质和平行四边形的判定与性质,掌握等边三角形的三个角都相等并且每个角都是60°;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
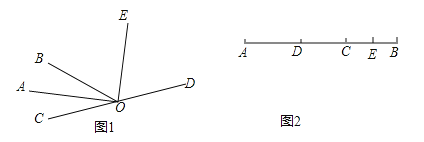
【题目】(1)如图1,已知O是直线CD上的点,OA平分∠BOC,OE平分∠BOD,∠AOC=35°,求∠BOE,∠COE的度数.
(2)如图2,已知AB=16cm,C是AB上一点,点D是线段AC的中点,点E是线段BC的中点,求线段DE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识的迁移与应用
问题一:甲、乙两车分别从相距180km的 A、B两地出发,甲车速度为36 km/h,乙车速度为24km/h,两车同时出发,相向而行, 后两车相距120 km?
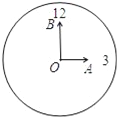
问题二:将线段弯曲后可视作钟表的一部分,如图,在一个圆形时钟的表面上,OA表示时针,OB表示分针(O为两针的旋转中心).下午3点时,OA与OB成直角.
(1)3:40时,时针与分针所成的角度 ;
(2)分针每分钟转过的角度为 ,时针每分钟转过的角度为 ;
(3)在下午3点至4点之间,从下午3点开始,经过多少分钟,时针与分针成60°角?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,动点P从点A出发,以1cm/s的速度向点D运动;动点Q从点C同时出发,以3cm/s的速度向点B运动.规定当其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t,求: 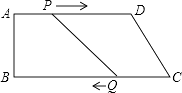
(1)当t为何值时,PQ∥CD?
(2)当t为何值时,PQ=CD?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个四边形的一条对角线把四边形分成两个等腰三角形,且其中一个等腰三角形的底角是另一个等腰三角形底角的2倍,我们把这条对角线叫做这个四边形的黄金线,这个四边形叫做黄金四边形.

(1)如图1,在四边形ABCD中,AB=AD=DC,对角线AC,BD都是黄金线,且AB<AC,CD<BD,求四边形ABCD各个内角的度数;
(2)如图2,点B是弧AC的中点,请在⊙O上找出所有的点D,使四边形ABCD的对角线AC是黄金线(要求:保留作图痕迹);
(3)在黄金四边形ABCD中,AB=BC=CD,∠BAC=30°,求∠BAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中注有“今两算得失相反,要令正负以名之.”意思是:“今有两数若其意义相反,则分别叫做正数和负数.”规定向东为正,向西为负.若向东走70m,记作+70m,则﹣20m表示( )
A.向西走20mB.向东走20mC.向西走50mD.向东走50m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH ,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )

A. 12 B. 15 C. 16 D. 18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com