
【题目】已知数轴上有A. B.C三点,分别表示有理数26,10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒。

(1)PA= ,PC= (用含t的代数式表示)
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,当点P运动到点C时,P、Q两点运动停止,
①当P、Q两点运动停止时,求点P和点Q的距离;
②求当t为何值时P、Q两点恰好在途中相遇.
【答案】(1)t;36-t;(2)①24;②30.
【解析】
(1)利用数轴上两点的距离公式求出AC的长度,根据路程=速度×时间,用t表示出AP,
再利用PC=AC-AP即可;
(2)①先利用数轴上两点的距离公式求出BC的长度,再利用时间=路程÷速度算出P从B运动到C的时间,算出Q的运动路程,最后减去AC即可;
②先利用AB的长度算出Q比P晚出发的时间,再利用P和Q运动总路程等于两个AC的长度列方程即可.
解:(1)由数轴可知:AC=10-(﹣26)=36个单位长度
∵动点P从A出发,以每秒1个单位的速度向终点C移动
PA=t,PC=36-t;
(2)①由数轴可知:BC=10-(﹣10)=20个单位长度,

∴P从B运动到C的时间为:20÷1=20s
∵当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动
∴当P从B运动到C时,Q的运动时间也是20s
∴Q的运动路程为:20×3=60个单位长度,
∵此时P在C处
∴QP=QC=60-AC=60-36=24.
②由数轴可知:AB=(﹣10)-(﹣26)=16个单位长度,

∵当点P运动到B点时,点Q从A点出发,
∴Q比P晚出发了:16÷1=16s
故Q的运动时间为(t-16)s,
由图可知:P和Q运动总路程等于两个AC的长度
∴t+3(t-16)=2×36
解得:t=30
答:当t等于30时,P、Q两点恰好在途中相遇


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.
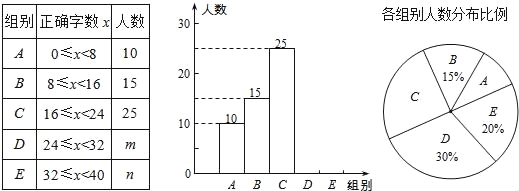
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是 ;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中A(0,a)、B(b,0),且满足4(a﹣2)2+![]() (b﹣4)2=0,点P(m,m)在线段AB上
(b﹣4)2=0,点P(m,m)在线段AB上
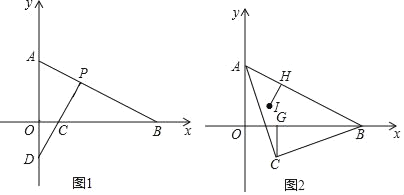
(1)求A、B的坐标;
(2)如图1,若过P作PC⊥AB交x轴于C,交y轴交于点D,求![]() 的值;
的值;
(3)如图2,以AB为斜边在AB下方作等腰直角△ABC,CG⊥OB于G,设I是∠OAB的角平分线与OP的交点,IH⊥AB于H.请探究![]() 的值是否发生改变,若不改变请求其值;若改变请说明理由.
的值是否发生改变,若不改变请求其值;若改变请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东70°的方向上.
(1)求从灯塔P看两轮船的视角(即∠APB)的度数?
(2)轮船C在∠APB的角平分线上,则轮船C在灯塔P的什么方位?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的![]() 倍,所购数量比第一批多100套.
倍,所购数量比第一批多100套.
(1)求第一批套尺购进时单价是多少?
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,P为BC边上任意一点,PF⊥AB于F,PE⊥AC于E,若AC边上的高BD=a.
(1)试说明PE+PF=a;
(2)若点P在BC的延长线上,其它条件不变,上述结论还成立吗?如果成立请说明理由;如果不成立,请重新给出一个关于PE,PF,a的关系式,不需要说明理由.
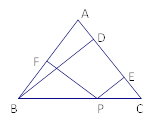
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索发现:
(1)计算:当a 4, b 3时, a2 b2 ; (a b)(a b) 。
当a 1, b 2 时, a2 b2 ; (a b)(a b) 。
(2)你能从上面的计算中发现什么结论? 。
(3)利用你发现的结论,求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入相应的数集中:
+1![]() 、-5%、200、-3、6.8、0、-
、-5%、200、-3、6.8、0、-![]() 、0.12003407、1、-43.555、77%、-3
、0.12003407、1、-43.555、77%、-3![]()
(1)非负数集合:______________________(2)负有理数集合:________________________
(3)正整数集合:______________________(4)负分数集合:___________________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com