
【题目】如图1,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
(1)用含a的式子表示花圃的面积.
(2)如果通道所占面积是整个长方形空地面积的![]() ,求出此时通道的宽.
,求出此时通道的宽.
(3)已知某园林公司修建通道、花圃的造价![]() (元)、
(元)、![]() (元)与修建面积x(m2)之间的函数关系如图2所示,如果学校决定由该公司承建此项目,并要求修建的通道的宽度不少于2米且不超过10米,那么通道宽为多少时,修建的通道和花圃的总造价最低,最低总造价为多少元?
(元)与修建面积x(m2)之间的函数关系如图2所示,如果学校决定由该公司承建此项目,并要求修建的通道的宽度不少于2米且不超过10米,那么通道宽为多少时,修建的通道和花圃的总造价最低,最低总造价为多少元?
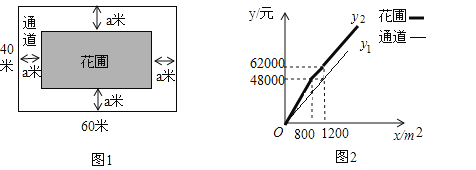
【答案】(1)(40﹣2a)(60﹣2a);(2)5;(3)当通道宽为2米时,修建的通道和花圃的总造价最低为23040元.
【解析】
试题分析:(1)用含a的式子先表示出花圃的长和宽,再利用其矩形面积公式列出式子即可;
(2)根据通道所占面积是整个长方形空地面积的![]() ,列方程解答即可;
,列方程解答即可;
(3)根据图象,设出通道和花圃的解析式,用待定系数法求解,再根据实际问题写出自变量的取值范围即可.
试题解析:(1)由图可知,花圃的面积为(40﹣2a)(60﹣2a);
(2)由已知可列式:60×40﹣(40﹣2a)(60﹣2a)=![]() ×60×40,解以上式子可得:
×60×40,解以上式子可得:![]() ,
,![]() (舍去),
(舍去),
答:所以通道的宽为5米;
(3)设修建的道路和花圃的总造价为y,由已知得![]() ,
,![]() ,
,
则![]() ;x花圃=(40﹣2a)(60﹣2a)=
;x花圃=(40﹣2a)(60﹣2a)=![]() ;x通道=60×40﹣(40﹣2a)(60﹣2a)=
;x通道=60×40﹣(40﹣2a)(60﹣2a)=![]() ,当2≤a≤10,800≤x花圃≤2016,384≤x通道≤1600,∴384≤x≤2016,所以当x取384时,y有最小值,最小值为2040,即总造价最低为23040元,当x=383时,即通道的面积为384时,有
,当2≤a≤10,800≤x花圃≤2016,384≤x通道≤1600,∴384≤x≤2016,所以当x取384时,y有最小值,最小值为2040,即总造价最低为23040元,当x=383时,即通道的面积为384时,有![]() =384,解得
=384,解得![]() ,
,![]() (舍去),所以当通道宽为2米时,修建的通道和花圃的总造价最低为23040元.
(舍去),所以当通道宽为2米时,修建的通道和花圃的总造价最低为23040元.


科目:初中数学 来源: 题型:
【题目】为发展旅游经济,我市某景区对门票釆用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分 的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.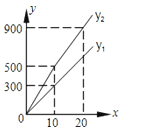
(1)观察图象求a,b,m的值
(2)直接写出y1 , y2与x之间的函数关系式;
(3)某旅行社导游王娜于5月1日带A团,5月20日(非节假日)带B团都到该景区旅游,共付门票款1900元,A,B两个团队合计50人,求A,B两个团队各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A,B的坐标分别为(3,m),(3,m+2),直线y=2x+b与线段AB有公共点,则b的取值范围为____________(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,错误的是( )
A.有一组邻边相等的平行四边形是菱形
B.两条对角线互相垂直且平分的四边形是菱形
C.对角线相等的平行四边形是矩形
D.有一组邻边相等的菱形是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com