
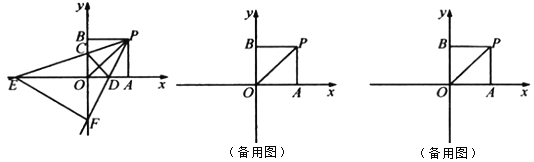
【题目】如图,在平面直角坐标系中,正方形![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() 轴正半轴与
轴正半轴与![]() 轴正半轴上,
轴正半轴上,![]() 是对角线.点
是对角线.点![]() 从
从![]() 点出发向
点出发向![]() 点运动(不与点
点运动(不与点![]() ,
,![]() 重合),到达
重合),到达![]() 点时停止运动,射线
点时停止运动,射线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连结
,连结![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)请探究:![]() 的面积是否变化?若不变化,试求出
的面积是否变化?若不变化,试求出![]() 的面积;若变化,请说明理由;
的面积;若变化,请说明理由;
(3)当![]() 为何值时,
为何值时,![]() 是等腰直角三角形;
是等腰直角三角形;
(4)过![]() 点作
点作![]() ,垂足为点
,垂足为点![]() ,请直接写出点
,请直接写出点![]() 运动的路线长.
运动的路线长.
【答案】(1)证明见解析; (2)三角形![]() 的面积=4,为定值;(3)
的面积=4,为定值;(3)![]() ;(4)
;(4)![]() 运动的路线长为
运动的路线长为![]() .
.
【解析】
(1)由∠POB=∠POF+∠OPF=45°,∠POA=∠PEO+∠OPE=45°,∠EPF=∠EPO+∠OPD=45°,可得∠EPO=∠OFP,∠PEO=∠OPF;(2)由△POE∽△FOP,可得![]() ,推出OP2=OEOF,由正方形OAPB的边长为2,推出OP=2
,推出OP2=OEOF,由正方形OAPB的边长为2,推出OP=2![]() ,推出OEOF=8,由此即可解决问题;(3)分两种情形讨论求解即可;(4)确定点G的运动轨迹,利用弧长公式计算即可.
,推出OEOF=8,由此即可解决问题;(3)分两种情形讨论求解即可;(4)确定点G的运动轨迹,利用弧长公式计算即可.
(1)证明:如图1中,
∵四边形OAPB是正方形,
∴∠POB=∠POA=45°,
∵∠POB=∠POF+∠OPF=45°,∠POA=∠PEO+∠OPE=45°,∠EPF=∠EPO+∠OPD=45°,
∴∠EPO=∠OFP,∠PEO=∠OPF,
∴△POE∽△FOP;
(2)解:结论:△OEF的面积是定值,不变;
理由:∵△POE∽△FOP,
∴![]() ,
,
∴OP2=OEOF,
∵正方形OAPB的边长为2,
∴OP=2![]() ,
,
∴OEOF=8,
∴S△OEF=![]() OEOF=4.
OEOF=4.
(3)如图2中,当FP=FE,∠PFE=90°时,易证△FBP≌△EOF,
∴OF=BP=2,OE=BF=4,
∵PB∥EO,
∴![]() ,
,
∴OC=![]() ,BC=
,BC=![]() ,
,
∴m=![]() .
.
如图3中,当PE=FE,∠PPEF=90°时,易证△FOD≌△EAP,
∴OE=AP=2,OF=AE=4,
∵PB∥EO,
∴![]() =1,
=1,
∴OC=![]() BC=1,
BC=1,
∴m=1,
综上所述,满足条件的m的值为![]() 或1.
或1.
(4)如图4中,将△PAD绕点P顺时针旋转90°得到△PBK.
易证△CPD≌△CPK,
∵PG⊥CD,PB⊥CK,
∴PG=PB=2,
∴点G的运动轨迹是以P为圆心2为半径的弧BD,
∴点G运动的路线长=![]() =π.
=π.


科目:初中数学 来源: 题型:
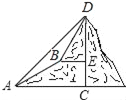
【题目】已知:如图,在山脚的A处测得山顶D的仰角为45°,沿着坡度为30°的斜角前进400米处到B处(即∠BAC=30°,AB=400米),测得D的仰角为60°,求山的高度CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个钢筋三角架三边长分别为![]() ,
,![]() ,
,![]() ,现在要做一个和它相似的钢筋三角架,而只有长为
,现在要做一个和它相似的钢筋三角架,而只有长为![]() 和
和![]() 的两根钢筋,要求以其中的一根为一边,从另一根上截两段(允许有余料)作为另两边,则不同的截法有( )
的两根钢筋,要求以其中的一根为一边,从另一根上截两段(允许有余料)作为另两边,则不同的截法有( )
A. 一种 B. 两种 C. 三种 D. 四种或四种以上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学全体学生1100人参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,结合图中所给信息解答下列问题:
(1)填写下表:
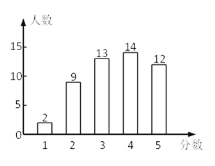
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩(单位:分) |
(2)估计光明中学全体学生社会实践活动成绩的总分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,二次函数![]() 中的
中的![]() ,
,![]() 满足下表.
满足下表.
| ... |
|
|
|
|
| ... |
| ... |
|
|
|
|
| ... |
(1)求该二次函数的解析式;
(2)![]() 的值等于多少;
的值等于多少;
(3)若![]() 、
、![]() 两点都在该函数的图象上,且
两点都在该函数的图象上,且![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
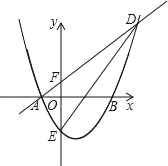
【题目】如图,抛物线![]() 与x轴交于A(-1,0)和B(3,0)两点,交y轴于点E.
与x轴交于A(-1,0)和B(3,0)两点,交y轴于点E.
(1)求此抛物线的解析式.
(2)若直线y=x+1与抛物线交于A、D两点,与y轴交于点F,连接DE,求△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数的图象与x轴的两个交点分别为(﹣1,0),(3,0),对于下列结论:①2a+b=0;②abc<0;③a+b+c>0;④当x>1时,y随x的增大而减小;其中正确的有( )
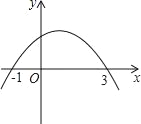
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
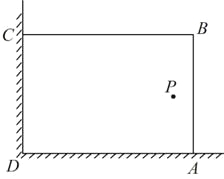
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2, 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
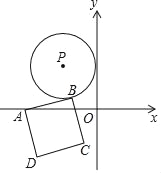
【题目】如图,在平面直角坐标系xOy中,以点P(﹣3,4)为圆心的⊙P与y轴相切,A是x轴上一动点,过A点的直线与⊙P相切于点B,以AB为边作正方形ABCD,则正方形ABCD面积的最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com