
【题目】如图,在△ABC中,BA=BC,以AB为直径作半圆⊙O,交AC于点D,过点D作DE⊥BC,垂足为点E.
(1)求证:DE为⊙O的切线;
(2)求证:BD2=ABBE.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)连接OD、BD,根据圆周角定理可得∠ADB=90°,继而得出点D是AC中点,判断出OD是三角形ABC的中位线,利用中位线的性质得出∠ODE=90°,这样可判断出结论.
(2)根据题意可判断△BED∽△BDC,从而可得BD2=BCBE,将BC替换成AB即可得出结论.
证明:(1)连接OD、BD,则∠ADB=90°(圆周角定理),
∵BA=BC,
∴CD=AD(三线合一),
又∵AO=OB,
∴OD是△ABC的中位线,
∴OD∥BC,
∵∠DEB=90°,
∴∠ODE=90°,即OD⊥DE,
故可得DE为⊙O的切线;
(2)∵∠EBD=∠DBC,∠DEB=∠CDB,
∴△BED∽△BDC,
∴![]() ,
,
又∵AB=BC,
∴![]() ,
,
故BD2=ABBE.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:

根据以上数据,估算袋中的白棋子数量为( )
A. 60枚B. 50枚C. 40枚D. 30枚
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,点E为AB的中点.
(1)求证:△ADC∽△ACB.
(2)若AD=2,AB=3,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0),tan∠BAC=![]() .
.
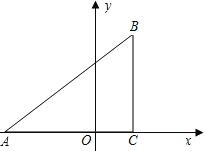
(1)求过点A,B的直线的函数表达式;
(2)在x轴上找一点D,连接BD,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;
(3)在(2)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m使得△APQ与△ADB相似?如存在,请求出的m值;如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AD>AB.

(1)作出∠ABC的平分线(尺规作图,保留作图痕迹,不写作法);
(2)若(1)中所作的角平分线交AD于点E,AF⊥BE,垂足为点O,交BC于点F,连接EF.求证:四边形ABFE为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张扑克牌的点数分别是2、3、4、8,将它们洗匀后背面朝上放在桌面上.
(1)从中随机抽取一张牌,求这张牌的点数是偶数的概率;
(2)从中先随机抽取一张牌,接着再抽取一张牌,求这两张牌的点数都是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC=α,∠DBC=β,且α+β=120°,连接AD,求∠ADB的度数.(不必解答)
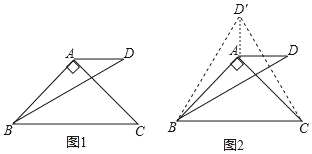
(1)小聪先从特殊问题开始研究,当α=90°,β=30°时,利用轴对称知识,以AB为对称轴构造△ABD的轴对称图形△ABD′,连接CD′(如图2),然后利用α=90°,β=30°以及等边三角形等相关知识便可解决这个问题.
请结合小聪研究问题的过程和思路,在这种特殊情况下填空:△D′BC的形状是 三角形;∠ADB的度数为 .
(2)在原问题中,当∠DBC<∠ABC(如图1)时,请计算∠ADB的度数;
(3)在原问题中,过点A作直线AE⊥BD,交直线BD于E,其他条件不变若BC=7,AD=2.请直接写出线段BE的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com