
【题目】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0),tan∠BAC=![]() .
.
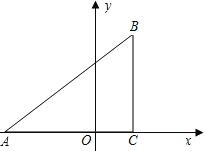
(1)求过点A,B的直线的函数表达式;
(2)在x轴上找一点D,连接BD,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;
(3)在(2)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m使得△APQ与△ADB相似?如存在,请求出的m值;如不存在,请说明理由.
【答案】(1)B(1,3);(2)D(![]() ,0);(3)这样的m存在.m=
,0);(3)这样的m存在.m=![]() .
.
【解析】
试题(1)根据点A、C的坐标求出AC的长,根据题意求出点B的坐标,利用待定系数法求出过点A,B的直线的函数表达式;(2)过点B作BD⊥AB,交x轴于点D,根据相似三角形的性质列出比例式,计算即可;(3)分PQ∥BD时和PQ⊥AD时两种情况,根据相似三角形的性质列出比例式,计算即可.
试题解析:(1)∵点A(3,0),C(1,0),
∴AC=4,又BC=![]() AC,
AC,
∴BC=3,
∴B点坐标为(1,3),
设过点A,B的直线的函数表达式为:y=kx+b,
则![]() ,
,
解得![]() ,
,
∴直线AB的函数表达式为:y=![]() x+
x+![]() ;
;
(2)如图1,过点B作BD⊥AB,交x轴于点D,
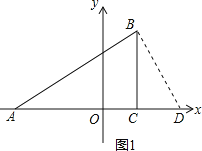
∵∠A=∠A,∠ABD=∠ACB,
∴△ADB∽△ABC,
∴D点为所求,
∵△ADB∽△ABC,
∴![]() ,即
,即![]() =
=![]() ,
,
解得,CD=![]() ,
,
∴OD=OC+CD=![]() ,
,
∴点D的坐标为(![]() ,0);
,0);
(3)在Rt△ABC中,由勾股定理得AB=![]() =5,
=5,
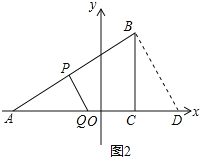
如图2,当PQ∥BD时,△APQ∽△ABD,
则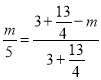 ,
,
解得,m=![]() ,
,
如图3,当PQ⊥AD时,△APQ∽△ADB,
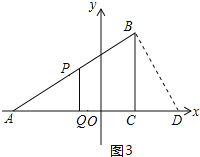
则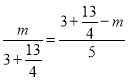 ,
,
解得,m=![]() ,
,
所以若△APQ与△ADB相似时,m=![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ACB=90°,AC > BC,CD是Rt△ABC的高,E是AC的中点,ED的延长线与CB的延长线相交于点F.
(1)求证:DF是BF和CF的比例中项;
(2)在AB上取一点G,如果AE·AC=AG·AD,求证:EG·CF=ED·DF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011贵州安顺)一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这条河的宽度.(参考数值:tan31°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是边长为3的等边△ABC边AB上一动点,沿过点P的直线折叠∠B,使点B落在AC上,对应点为D,折痕交BC于E,点D是AC的一个三等分点,PB的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径作半圆⊙O,交AC于点D,过点D作DE⊥BC,垂足为点E.
(1)求证:DE为⊙O的切线;
(2)求证:BD2=ABBE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球赛期间,某商店销售一批足球纪念册,每本进价40元,规定销售单价不低于44元,且获利不高于30%.试销售期间发现,当销售单价定为44元时,每天可售出300本,销售单价每涨1元,每天销售量减少10本,现商店决定提价销售.设每天销售为![]() 本,销售单价为
本,销售单价为![]() 元.
元.
(1)请直接写出![]() 与
与![]() 之间的函数关系式和自变量
之间的函数关系式和自变量![]() 的取值范围;
的取值范围;
(2)将足球纪念册销售单价定为多少元时,商店每天销售纪念册获得的利润![]() 元最大?最大利润是多少元?
元最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有甲、乙两座楼房,楼间距BC为50米,在乙楼顶部A点测得甲楼顶部D点的仰角为37°,在乙楼底部B点测得甲楼顶部D点的仰角为60°,则甲、乙两楼的高度分别为多少?(结果精确到1米,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com