
【题目】(2011贵州安顺)一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这条河的宽度.(参考数值:tan31°≈![]() )
)

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】当今,越来越多的青少年在观看影片《流浪地球》后,更加喜欢同名科幻小说,该小说销量也急剧上升.书店为满足广大顾客需求,订购该科幻小说若干本,每本进价为20元.根据以往经验:当销售单价是25元时,每天的销售量是250本;销售单价每上涨1元,每天的销售量就减少10本,书店要求每本书的利润不低于10元且不高于18元.
(1)直接写出书店销售该科幻小说时每天的销售量![]() (本)与销售单价
(本)与销售单价![]() (元)之间的函数关系式及自变量的取值范围.
(元)之间的函数关系式及自变量的取值范围.
(2)书店决定每销售1本该科幻小说,就捐赠![]() 元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求
元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:

根据以上数据,估算袋中的白棋子数量为( )
A. 60枚B. 50枚C. 40枚D. 30枚
查看答案和解析>>
科目:初中数学 来源: 题型:
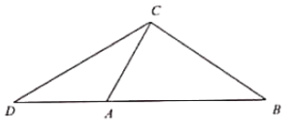
【题目】如图,已知在![]() 中,∠ACB=90°,
中,∠ACB=90°,![]() ,延长边BA至点D,使AD=AC,联结CD.
,延长边BA至点D,使AD=AC,联结CD.
(1)求∠D的正切值;
(2)取边AC的中点E,联结BE并延长交边CD于点F,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,∠C=90°,点O在AC上,以AO为半径的⊙O交AB于D, BD的垂直平分线交BD于F,交BC于E,连接DE.

(1)求证:DE是⊙O的切线;
(2)若∠B=30°,BC=![]() ,且AD∶DF=1∶2,求⊙O的直径.
,且AD∶DF=1∶2,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
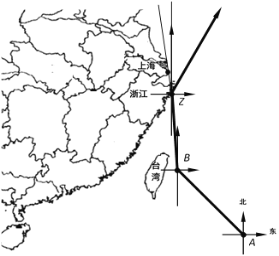
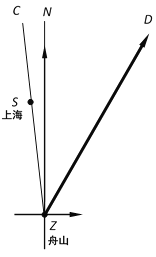
【题目】2019年第18号台风“米娜”于9月29日早晨5点整,由位于台湾省周边的B岛东南方约980千米的西北太平洋洋面上(A点)生成,向西北方向移动.并于9月30日20时30分到达B岛后风力增强且转向,一路向北于24小时后在浙江省舟山市登陆.“米娜”在登录后风力减弱且再一次转向,以每小时20千米的速度向北偏东30的方向移动,距台风中心170千米的范围内是受台风影响的区域.已知上海位于舟山市北偏西7方向,且距舟山市250千米.
(1)台风中心从生成点(A点)到达B岛的速度是每小时多少千米?
(2)10月2日上海受到“米娜”影响,那么上海遭受这次台风影响的时间有多长?(结果保留整数,参考数据:![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,点E为AB的中点.
(1)求证:△ADC∽△ACB.
(2)若AD=2,AB=3,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0),tan∠BAC=![]() .
.
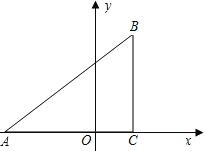
(1)求过点A,B的直线的函数表达式;
(2)在x轴上找一点D,连接BD,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;
(3)在(2)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m使得△APQ与△ADB相似?如存在,请求出的m值;如不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com