
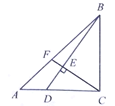
【题目】如图,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() 为边
为边![]() 上一点,且
上一点,且![]() ,连结
,连结![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .若
.若![]() ,则
,则![]() 的长为______.
的长为______.
【答案】![]()
【解析】
作AH⊥BD的延长线于点H,根据已知和勾股定理可求出CD,AD,AB,再根据三角形面积公式,可求出CE的长度,进而可求ED,BE,然后证得△AHD∽△CED,△BEF∽△BHA,根据相似比即可求出答案.
作AH⊥BD的延长线于点H,
∵BC=AC=6,CD=2AD,
∴AD=2,CD=4,
根据勾股定理AB=![]() ,BD=
,BD=![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵CE⊥BD,
∴根据勾股定理可得ED=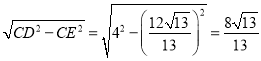 ,
,
∴![]() ,
,
在△AHD与△CED中,∠AHD=∠CED,∠ADH=∠CDE,
∴△AHD∽△CED,
∴![]() ,
,
∴![]() ,
,
根据勾股定理得 ,
,
∴![]() ,
,
在△BEF与△BHA中,∠FBE=∠ABH,∠BEF=∠BHA=90°,
∴△BEF∽△BHA,
∴![]() ,
,
∴![]() ,
,
故答案为![]() .
.



 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】(2011贵州安顺)一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这条河的宽度.(参考数值:tan31°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径作半圆⊙O,交AC于点D,过点D作DE⊥BC,垂足为点E.
(1)求证:DE为⊙O的切线;
(2)求证:BD2=ABBE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球赛期间,某商店销售一批足球纪念册,每本进价40元,规定销售单价不低于44元,且获利不高于30%.试销售期间发现,当销售单价定为44元时,每天可售出300本,销售单价每涨1元,每天销售量减少10本,现商店决定提价销售.设每天销售为![]() 本,销售单价为
本,销售单价为![]() 元.
元.
(1)请直接写出![]() 与
与![]() 之间的函数关系式和自变量
之间的函数关系式和自变量![]() 的取值范围;
的取值范围;
(2)将足球纪念册销售单价定为多少元时,商店每天销售纪念册获得的利润![]() 元最大?最大利润是多少元?
元最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.
(1)求证:![]() ;
;
(2)若AB⊥AC,AE:EC=1:2,F是BC中点,求证:四边形ABFD是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
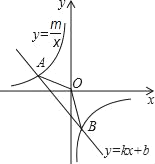
【题目】如图,已知A(4,2)、B(n,﹣4)是一次函数y=kx+b图象与反比例函数![]() 图象的两个交点.
图象的两个交点.
(1)求此反比例函数和一次函数的解析式;
(2)直接写出△AOB的面积;
(3)根据图象直接写出使一次函数的值小于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有甲、乙两座楼房,楼间距BC为50米,在乙楼顶部A点测得甲楼顶部D点的仰角为37°,在乙楼底部B点测得甲楼顶部D点的仰角为60°,则甲、乙两楼的高度分别为多少?(结果精确到1米,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,将腰CD以D为中心逆时针旋转90°至DE,连结AE、CE,△ADE的面积为12,则BC的长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com