
【题目】如图,已知A(4,2)、B(n,﹣4)是一次函数y=kx+b图象与反比例函数![]() 图象的两个交点.
图象的两个交点.
(1)求此反比例函数和一次函数的解析式;
(2)直接写出△AOB的面积;
(3)根据图象直接写出使一次函数的值小于反比例函数的值的x的取值范围.
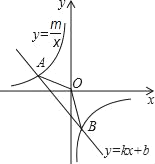
【答案】(1)y=﹣![]() ,y=﹣x﹣2;(2)S△AOB=6;(3)﹣4<x<0或x>2.
,y=﹣x﹣2;(2)S△AOB=6;(3)﹣4<x<0或x>2.
【解析】
(1)利用待定系数法即可求出函数的解析式;
(2)由(1)求出的一次函数解析式求出AB与x轴的交点坐标(-2,0),从而将△AOB分解为两个底边长为2的三角形,然后结合A、B两点纵坐标求出各自三角形面积,最后相加即可;
(3)根据一次函数的值小于反比例函数的值的x的取值范围就是对应的一次函数图像在反比例函数图像下方的自变量的取值范围求解即可.
解:(1)把(﹣4,2)代入y=![]() 得2=
得2=![]() ,则m=﹣8.
,则m=﹣8.
则反比例函数的解析式是y=﹣![]() ;
;
把(n,﹣4)代入y=﹣![]() 得n=﹣
得n=﹣![]() =2,
=2,
则B的坐标是(2,﹣4).
根据题意得:![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,,
,,
∴一次函数的解析式是y=﹣x﹣2;
(2)设AB与x轴的交点是C,则C的坐标是(﹣2,0).
则OC=2,
S△AOC=2,S△BOC=4,
则S△AOB=6;
(3)由函数图象可知x的取值范围时﹣4<x<0或x>2.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,点E为AB的中点.
(1)求证:△ADC∽△ACB.
(2)若AD=2,AB=3,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(﹣1,0),B(3,0),C(0,3)三点.
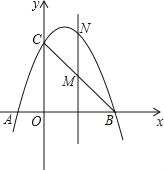
(1)求抛物线的解析式;
(2)点M是线段BC上的点(不与B、C重合),过M作NM∥y轴交抛物线于N,若点M的横坐标为m,请用含m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点m,使△BNC的面积最大?若存在,求m的值和△BNC的面积;若不存在,说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.给出以下结论:①DG=DF;②四边形EFDG是菱形;③EG2=![]() GF×AF;④当AG=6,EG=2
GF×AF;④当AG=6,EG=2![]() 时,BE的长为
时,BE的长为![]() ,其中正确的编号组合是( )
,其中正确的编号组合是( )
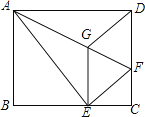
A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (x>0)的图象与直线y=x交于点M,∠AMB=90°,其两边分别与两坐标轴的正半轴交于点A、B,四边形OAMB的面积为6.
(x>0)的图象与直线y=x交于点M,∠AMB=90°,其两边分别与两坐标轴的正半轴交于点A、B,四边形OAMB的面积为6.
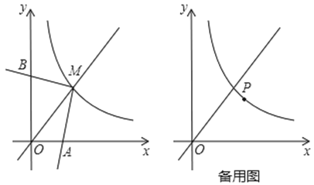
(1)求k的值;
(2)点P在(1)的反比例函数y=![]() (x>0)的图象上,若点P的横坐标为3,在x轴上有一点D(4,0),若在直线y=x上有动点C,构成△PDC,其面积为3,请写出C点的坐标;
(x>0)的图象上,若点P的横坐标为3,在x轴上有一点D(4,0),若在直线y=x上有动点C,构成△PDC,其面积为3,请写出C点的坐标;
(3)若∠EPF=90°,其两边分别为与x轴正半轴,直线y=x交于点E、F,问是否存在点E,使PE=PF?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC=α,∠DBC=β,且α+β=120°,连接AD,求∠ADB的度数.(不必解答)
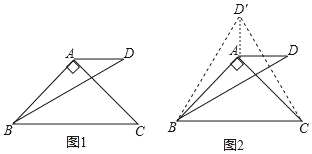
(1)小聪先从特殊问题开始研究,当α=90°,β=30°时,利用轴对称知识,以AB为对称轴构造△ABD的轴对称图形△ABD′,连接CD′(如图2),然后利用α=90°,β=30°以及等边三角形等相关知识便可解决这个问题.
请结合小聪研究问题的过程和思路,在这种特殊情况下填空:△D′BC的形状是 三角形;∠ADB的度数为 .
(2)在原问题中,当∠DBC<∠ABC(如图1)时,请计算∠ADB的度数;
(3)在原问题中,过点A作直线AE⊥BD,交直线BD于E,其他条件不变若BC=7,AD=2.请直接写出线段BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
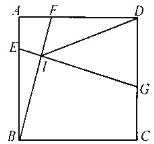
【题目】如图,在边长为6的正方形ABCD中,点E、F、G分别在边AB、AD、CD上,EG与BF交于点I,AE=2,BF=EG,DG>AE,则DI的最小值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com