
����Ŀ����ͼ������������y��![]() ��x��0����ͼ����ֱ��y��x���ڵ�M����AMB��90���������߷ֱ�����������������ύ�ڵ�A��B���ı���OAMB�����Ϊ6��
��x��0����ͼ����ֱ��y��x���ڵ�M����AMB��90���������߷ֱ�����������������ύ�ڵ�A��B���ı���OAMB�����Ϊ6��
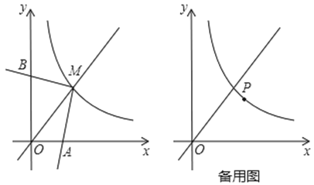
��1����k��ֵ��
��2����P�ڣ�1���ķ���������y��![]() ��x��0����ͼ���ϣ�����P�ĺ�����Ϊ3����x������һ��D��4��0��������ֱ��y��x���ж���C��������PDC�������Ϊ3����д��C������ꣻ
��x��0����ͼ���ϣ�����P�ĺ�����Ϊ3����x������һ��D��4��0��������ֱ��y��x���ж���C��������PDC�������Ϊ3����д��C������ꣻ
��3������EPF��90���������߷ֱ�Ϊ��x�������ᣬֱ��y��x���ڵ�E��F�����Ƿ���ڵ�E��ʹPE��PF�������ڣ������E�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��k��6����2�����������ĵ�C����Ϊ![]() ��
��![]() ����3�����ڣ���4��0���ͣ�6��0��
����3�����ڣ���4��0���ͣ�6��0��
��������
��1������M��MC��x���ڵ�C��MD��y���ڵ�D������AAS֤����AMC�ա�BMD����ôS�ı���OCMD=S�ı���OAMB=6�����ݷ�������������ϵ��k�ļ�������ó�k=6��
��2����ͼ1-1�У��ӳ�DP��OC�ڵ�E����DH��OC��H�����������ε������ʽ���EC�ij����ɽ�����⣻
��3���ȸ��ݷ���������ͼ���ϵ������������õ�P������Ϊ��3��2�����ٷ���������������ۣ�����ͼ2������P��PG��x���ڵ�G������F��FH��PG�ڵ�H����y���ڵ�K������AAS֤����PGE�ա�FHP���������E�����ꣻ����ͼ3��ͬ�����E�����꣮
�⣺��1����ͼ1������M��MC��x���ڵ�C��MD��y���ڵ�D��

���MCA����MDB��90������AMC����BMD��MC��MD��
���AMC�ա�BMD��
��S�ı���OCMD��S�ı���OAMB��6��
��k��6��
��2����ͼ1��1�У��ӳ�DP��OC�ڵ�E����DH��OC��H����PJ��OC��J��

��D��4��0����P��3��2����
��ֱ��PD�Ľ���ʽΪy����2x+8��
��![]() �����
�����![]() ��
��
��E��![]() ��
��![]() ����
����
��Rt��ODH�У��ߡ�DOH��45����OD��4��
��DH��2![]() ��ͬ���ɵ�PJ��
��ͬ���ɵ�PJ��![]()
��![]() ECDH��
ECDH��![]() ECPJ��3��
ECPJ��3��
��EC��2![]() ��
��
�����������ĵ�C����Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() ����
����
��3�����ڵ�E��ʹ��PE��PF��
�����⣬�õ�P������Ϊ��3��2����
����ͼ2������P��PG��x���ڵ�G������F��FH��PG�ڵ�H����y���ڵ�K��
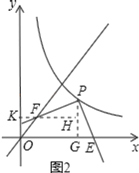
�ߡ�PGE����FHP��90������EPG����PFH��PE��PF��
���PGE�ա�FHP��
��PG��FH��2��FK��OK��3��2��1��GE��HP��2��1��1��
��OE��OG+GE��3+1��4��
��E��4��0����
����ͼ3������P��PG��x���ڵ�G������F��FH��PG�ڵ�H����y���ڵ�K��

�ߡ�PGE����FHP��90������EPG����PFH��PE��PF��
���PGE�ա�FHP��
��PG��FH��2��FK��OK��3+2��5��GE��HP��5��2��3��
��OE��OG+GE��3+3��6��
��E��6��0����
�ʴ�Ϊ��4��0���ͣ�6��0����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P�DZ߳�Ϊ3�ĵȱߡ�ABC��AB��һ���㣬�ع���P��ֱ���۵���B��ʹ��B����AC�ϣ���Ӧ��ΪD���ۺ۽�BC��E����D��AC��һ�����ȷֵ㣬PB�ij�Ϊ______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB=AD��AC��BD���ڵ�E����ADB=��ACB��
��1����֤��![]() ��
��
��2����AB��AC��AE��EC=1��2��F��BC�е㣬��֤���ı���ABFD�����Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
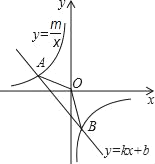
����Ŀ����ͼ����֪A��4��2����B��n����4����һ�κ���y��kx+bͼ���뷴��������![]() ͼ����������㣮
ͼ����������㣮
��1����˷�����������һ�κ����Ľ���ʽ��
��2��ֱ��д����AOB�������
��3������ͼ��ֱ��д��ʹһ�κ�����ֵС�ڷ�����������ֵ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���C��90������б��ABΪ��������������ABDE���������ζԽ��߽��ڵ�O������OC����֪AC��3��OC��6![]() ������һֱ�DZ�BC�ij�Ϊ_____��
������һֱ�DZ�BC�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijС���мס�������¥����¥���BCΪ50�ף�����¥����A���ü�¥����D�������Ϊ37��������¥�ײ�B���ü�¥����D�������Ϊ60������ס�����¥�ĸ߶ȷֱ�Ϊ���٣�(�����ȷ��1�ף�sin37���0.60��cos37���0.80��tan37���0.75��![]() ��1.73)
��1.73)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
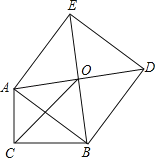
����Ŀ����ͼ����ABC�ڽ��ڡ�O����AB��AC���ӳ�BC����D��ʹCD��CA������AD����O���E������BE��CE.
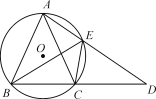
(1)��֤����ABE�ա�CDE��
(2)��գ�
�ٵ���ABC�Ķ���Ϊ______ʱ���ı���AOCE�����Σ�
����AE��![]() ��AB��2
��AB��2![]() ����DE�ij�Ϊ______��
����DE�ij�Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��һ���������У�������������x��y��ʹ��y��x2����ƴ�������Ϊ��ƽ������������x��Ϊƽ���ߣ�
��1�������ȱ�������Ϊƽ�������Σ������Ϊ![]() ���� �����⣻����һ����Ϊ30������һ��ֱ�DZ�Ϊ2��ֱ����������ƽ�������������� �����⣻��������������������
���� �����⣻����һ����Ϊ30������һ��ֱ�DZ�Ϊ2��ֱ����������ƽ�������������� �����⣻��������������������
��2����a��b��c��ƽ�������ε������ߣ�ƽ����a��2�����������д���һ����Ϊ60������c��ֵ��
��3����ͼ������ABC�У�D��BC��һ�㣮
������CAD����B��CD��1����֤����ABC��ƽ�������Σ�
������C��90����BD��1��AC��m��CD��n����tan��DAB�����ú�m��n�Ĵ���ʽ��ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() �ֱ����ı���
�ֱ����ı���![]() ��
��![]() �ĶԽ��ߣ���
�ĶԽ��ߣ���![]() ��
��![]() �ڣ�
�ڣ�![]() .
.
��1����ͼ1�����ı���![]() ��
��![]() ��Ϊ������ʱ������
��Ϊ������ʱ������![]() .
.
����֤��![]() ��
��![]() ��
��
����![]() ��
��![]() ����
����![]() �ij���
�ij���
��2����ͼ2�����ı���![]() ��
��![]() ��������
��Ϊ���Σ���![]() ʱ����
ʱ����![]() ��
��![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��
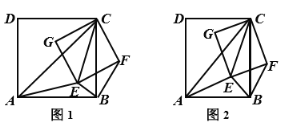
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com