
 如图,在正方形ABCD外取一点E,连接AE,DE,BE,过点A作AE的垂线交ED于点P,连接BP,AE=AP=1,PB=$\sqrt{5}$,有下列结论:
如图,在正方形ABCD外取一点E,连接AE,DE,BE,过点A作AE的垂线交ED于点P,连接BP,AE=AP=1,PB=$\sqrt{5}$,有下列结论:| A. | ①③④ | B. | ①②⑤ | C. | ③④⑤ | D. | ①③⑤ |
分析 ①利用同角的余角相等,易得∠EAB=∠PAD,再结合已知条件利用SAS可证两三角形全等;
②过B作BF⊥AE,交AE的延长线于F,利用③中的∠BEP=90°,利用勾股定理可求BE,结合△AEP是等腰直角三角形,可证△BEF是等腰直角三角形,再利用勾股定理可求EF、BF;
③利用①中的全等,可得∠APD=∠AEB,结合三角形的外角的性质,易得∠BEP=90°,即可证;
④连接BD,求出△ABD的面积,然后减去△BDP的面积即可;
⑤在Rt△ABF中,利用勾股定理可求AB2,即是正方形的面积.
解答 解:①∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,
∴∠EAB=∠PAD,
又∵AE=AP,AB=AD,
∵在△APD和△AEB中,$\left\{\begin{array}{l}{AE=AP}&{\;}\\{∠EAB=∠PAD}&{\;}\\{AB=AD}&{\;}\end{array}\right.$,
∴△APD≌△AEB(SAS);
故此选项正确;
③∵△APD≌△AEB,
∴∠APD=∠AEB,
∵∠AEB=∠AEP+∠BEP,∠APD=∠AEP+∠PAE,
∴∠BEP=∠PAE=90°,
∴EB⊥ED;故此选项正确;
②过B作BF⊥AE,交AE的延长线于F,
∵AE=AP,∠EAP=90°,
∴∠AEP=∠APE=45°,PE=$\sqrt{2}$AE=$\sqrt{2}$,
又∵③中EB⊥ED,BF⊥AF,
∴∠FEB=∠FBE=45°,
又∵BE=$\sqrt{P{B}^{2}-P{E}^{2}}$=$\sqrt{3}$,
∴BF=EF=$\frac{\sqrt{3}}{\sqrt{2}}$=$\frac{\sqrt{6}}{2}$,
故此选项错误;
④如图,连接BD,在Rt△AEP中,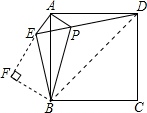
∵AE=AP=1,
∴EP=$\sqrt{2}$,
又∵PB=$\sqrt{5}$,
∴BE=$\sqrt{3}$,
∵△APD≌△AEB,
∴PD=BE=$\sqrt{3}$,
∴S△ABP+S△ADP=S△ABD-S△BDP=$\frac{1}{2}$S正方形ABCD-$\frac{1}{2}$×DP×BE=$\frac{1}{2}$×(4+$\sqrt{6}$)-$\frac{1}{2}$×$\sqrt{3}$×$\sqrt{3}$=$\frac{1}{2}$+$\frac{\sqrt{6}}{2}$.
故此选项错误.
⑤∵EF=BF=$\frac{\sqrt{6}}{2}$,AE=1,
∴在Rt△ABF中,AB2=(AE+EF)2+BF2=4+$\sqrt{6}$,
∴S正方形ABCD=AB2=4+$\sqrt{6}$,
故此选项正确.
故选:B.
点评 本题考查了全等三角形的判定和性质的运用、正方形的性质的运用、正方形和三角形的面积公式的运用、勾股定理的运用等知识.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在网格图中,每格是边长为1的正方形,四边形ABCD的顶点均为格点.
如图,在网格图中,每格是边长为1的正方形,四边形ABCD的顶点均为格点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
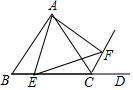 如图,在等边△ABC中,AB=4,点E在BC边上,将射线AE绕点A逆时针旋转60°,与△ABC的外角∠ACD的平分线交于点F,连接AF.设BE=x,△AEF的面积为y,则y与x之间的函数关系式为y=$\frac{\sqrt{3}}{4}$x2-$\sqrt{3}$x+4$\sqrt{3}$.
如图,在等边△ABC中,AB=4,点E在BC边上,将射线AE绕点A逆时针旋转60°,与△ABC的外角∠ACD的平分线交于点F,连接AF.设BE=x,△AEF的面积为y,则y与x之间的函数关系式为y=$\frac{\sqrt{3}}{4}$x2-$\sqrt{3}$x+4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
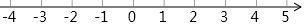 解不等式组$\left\{\begin{array}{l}{1-x>-2①}\\{2x+3≥x-1②}\end{array}\right.$
解不等式组$\left\{\begin{array}{l}{1-x>-2①}\\{2x+3≥x-1②}\end{array}\right.$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
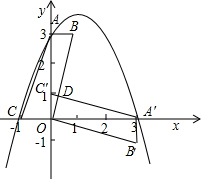 平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别为(0,3)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A'B'OC'.
平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别为(0,3)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A'B'OC'.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com