
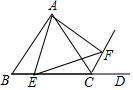
 如图,在等边△ABC中,AB=4,点E在BC边上,将射线AE绕点A逆时针旋转60°,与△ABC的外角∠ACD的平分线交于点F,连接AF.设BE=x,△AEF的面积为y,则y与x之间的函数关系式为y=$\frac{\sqrt{3}}{4}$x2-$\sqrt{3}$x+4$\sqrt{3}$.
如图,在等边△ABC中,AB=4,点E在BC边上,将射线AE绕点A逆时针旋转60°,与△ABC的外角∠ACD的平分线交于点F,连接AF.设BE=x,△AEF的面积为y,则y与x之间的函数关系式为y=$\frac{\sqrt{3}}{4}$x2-$\sqrt{3}$x+4$\sqrt{3}$. 分析 过A作AH⊥BC于H,根据等边三角形的性质得到AH=2$\sqrt{3}$,求得S△ABC=$\frac{1}{2}×$4×2$\sqrt{3}$=4$\sqrt{3}$,根据旋转的性质得到∠EAF=∠BAC=60°,根据全等三角形的性质得到CF=BE=x,过F作FG⊥BD于G,求得FG=$\frac{\sqrt{3}}{2}$x,推出S四边形AECF=S△ABC=4$\sqrt{3}$,于是得到结论.
解答 解:过A作AH⊥BC于H,
∵在等边△ABC中,AB=4,
∴AH=2$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}×$4×2$\sqrt{3}$=4$\sqrt{3}$,
∵射线AE绕点A逆时针旋转60°,
∴∠EAF=∠BAC=60°,
∴∠BAE=∠CAF,
∵CF平分∠ACD,∠ACD=120°,
∴∠ACF=∠DCF=60°,
在△ABE与△ACF中,$\left\{\begin{array}{l}{∠BAE=∠CAF}\\{AB=AC}\\{∠B=∠ACF}\end{array}\right.$,
∴△ABE≌△ACF,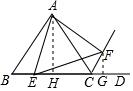
∴CF=BE=x,
过F作FG⊥BD于G,
∴FG=$\frac{\sqrt{3}}{2}$x,
∵CE=4-x,
∴S△ECF=$\frac{1}{2}$EC•FG=$\frac{1}{2}$(4-x)×$\frac{\sqrt{3}}{2}$x=$\sqrt{3}$x-$\frac{\sqrt{3}}{4}$x2,
∵△ABE≌△ACF,
∴S四边形AECF=S△ABC=4$\sqrt{3}$,
∴y=S四边形AECF-S△ECF=4$\sqrt{3}$-($\sqrt{3}$x-$\frac{\sqrt{3}}{4}$x2),
即y=$\frac{\sqrt{3}}{4}$x2-$\sqrt{3}$x+4$\sqrt{3}$.
故答案为:y=$\frac{\sqrt{3}}{4}$x2-$\sqrt{3}$x+4$\sqrt{3}$.
点评 本题考查了旋转的性质,全等三角形的判定与性质,等边三角形的性质,三角形的面积的计算,正确的作出辅助线是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
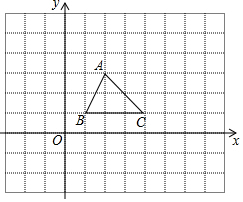 如图,在边长为1个单位长度的小正方形网格中,
如图,在边长为1个单位长度的小正方形网格中,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
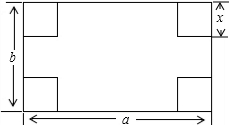 如图,小明想把一长为a,宽为b的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个边长为x的小正方形,用代数式表示纸片剩余部分的周长2a+2b+2x.
如图,小明想把一长为a,宽为b的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个边长为x的小正方形,用代数式表示纸片剩余部分的周长2a+2b+2x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
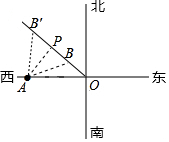 某号台风中心位于O地,台风中心以25km/h的速度向西北方向移动,在距台风中心240km的范围内将受到影响.城市A在O地正西方向与O地相距320km处,如图所示,则A市是否会遭受此台风的影响?若受影响,将有多长时间受影响?($\sqrt{2}$=1.414)
某号台风中心位于O地,台风中心以25km/h的速度向西北方向移动,在距台风中心240km的范围内将受到影响.城市A在O地正西方向与O地相距320km处,如图所示,则A市是否会遭受此台风的影响?若受影响,将有多长时间受影响?($\sqrt{2}$=1.414)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
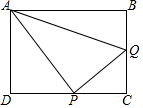 如图,已知矩形ABCD,AB=8cm,BC=6cm,点Q为BC中点,在DC上取一点P,使△APQ的面积等于18cm2,则DP的长度为4cm.
如图,已知矩形ABCD,AB=8cm,BC=6cm,点Q为BC中点,在DC上取一点P,使△APQ的面积等于18cm2,则DP的长度为4cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在正方形ABCD外取一点E,连接AE,DE,BE,过点A作AE的垂线交ED于点P,连接BP,AE=AP=1,PB=$\sqrt{5}$,有下列结论:
如图,在正方形ABCD外取一点E,连接AE,DE,BE,过点A作AE的垂线交ED于点P,连接BP,AE=AP=1,PB=$\sqrt{5}$,有下列结论:| A. | ①③④ | B. | ①②⑤ | C. | ③④⑤ | D. | ①③⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com