
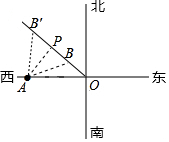
 某号台风中心位于O地,台风中心以25km/h的速度向西北方向移动,在距台风中心240km的范围内将受到影响.城市A在O地正西方向与O地相距320km处,如图所示,则A市是否会遭受此台风的影响?若受影响,将有多长时间受影响?($\sqrt{2}$=1.414)
某号台风中心位于O地,台风中心以25km/h的速度向西北方向移动,在距台风中心240km的范围内将受到影响.城市A在O地正西方向与O地相距320km处,如图所示,则A市是否会遭受此台风的影响?若受影响,将有多长时间受影响?($\sqrt{2}$=1.414) 分析 作AP⊥OB',易求得AP的长度,根据AP和240的大小可以判断A市受影响,受影响时间为台风中心在BB'距离时,求得BB'的长即可解题.
解答 解:作AP⊥OB',AB'=AB=240km,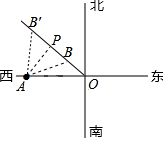
∵∠BOA=45°,
∴AP=320×$\frac{\sqrt{2}}{2}$=160$\sqrt{2}$km,
∵160$\sqrt{2}$≈226<240,
∴A市会遭受此台风的影响,
∵AB=240km,
∴PB=$\sqrt{A{B}^{2}-A{P}^{2}}$=$\sqrt{24{0}^{2}-(160\sqrt{2})^{2}}$=80km,
∴BB'=2PB=160km,
∴受到影响时间为$\frac{160}{25}$=6.4小时.
即A市受影响时间为6.4小时.
点评 本题考查了直角三角形的运用、勾股定理的运用,本题中求得BB'的长是解题的关键.


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在网格图中,每格是边长为1的正方形,四边形ABCD的顶点均为格点.
如图,在网格图中,每格是边长为1的正方形,四边形ABCD的顶点均为格点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,现有一架长4m的梯子AB斜靠在墙面上,要想使人安全地攀上梯子的顶端,梯子与地面所成的角α一般要满足50°≤α≤75°.
如图,现有一架长4m的梯子AB斜靠在墙面上,要想使人安全地攀上梯子的顶端,梯子与地面所成的角α一般要满足50°≤α≤75°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
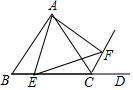 如图,在等边△ABC中,AB=4,点E在BC边上,将射线AE绕点A逆时针旋转60°,与△ABC的外角∠ACD的平分线交于点F,连接AF.设BE=x,△AEF的面积为y,则y与x之间的函数关系式为y=$\frac{\sqrt{3}}{4}$x2-$\sqrt{3}$x+4$\sqrt{3}$.
如图,在等边△ABC中,AB=4,点E在BC边上,将射线AE绕点A逆时针旋转60°,与△ABC的外角∠ACD的平分线交于点F,连接AF.设BE=x,△AEF的面积为y,则y与x之间的函数关系式为y=$\frac{\sqrt{3}}{4}$x2-$\sqrt{3}$x+4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组$\left\{\begin{array}{l}{1-x>-2①}\\{2x+3≥x-1②}\end{array}\right.$
解不等式组$\left\{\begin{array}{l}{1-x>-2①}\\{2x+3≥x-1②}\end{array}\right.$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
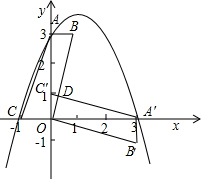 平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别为(0,3)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A'B'OC'.
平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别为(0,3)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A'B'OC'.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
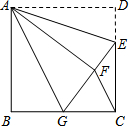 如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.G为BC上的一点,将△ADE沿AE对折至△AFE,同时将△ABG沿AG对折至△AFG,连接CF.
如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.G为BC上的一点,将△ADE沿AE对折至△AFE,同时将△ABG沿AG对折至△AFG,连接CF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com