
【题目】综合与实践:
如图1,![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() 且
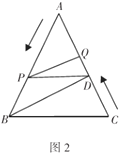
且![]() ;如图2,在图1的基础上,动点
;如图2,在图1的基础上,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 的速度沿线段
的速度沿线段![]() 向点
向点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发以相同速度沿线段
出发以相同速度沿线段![]() 向点
向点![]() 运动,当其中一点到达终点时另外一点也随之停止运动,设点
运动,当其中一点到达终点时另外一点也随之停止运动,设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
(1)求![]() 的长;
的长;
(2)当![]() 的其中一边与
的其中一边与![]() 平行时(
平行时(![]() 与
与![]() 不重合),求
不重合),求![]() 的值;
的值;
(3)点![]() 在线段
在线段![]() 上运动的过程中,是否存在以
上运动的过程中,是否存在以![]() 为腰的
为腰的![]() 是等腰三角形?若存在,求出
是等腰三角形?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.


【答案】(1)![]() ;(2)
;(2)![]() 的值为2.5秒或3秒;(3)存在,
的值为2.5秒或3秒;(3)存在,![]() 的值为3或
的值为3或![]() 秒.
秒.
【解析】
(1)设![]() ,
,![]() ,则
,则![]() ,在Rt△ABD中利用勾股定理建立方程求出x,即可得到AB的长;
,在Rt△ABD中利用勾股定理建立方程求出x,即可得到AB的长;
(2)分两种情况讨论:①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ,分别建立方程求解;
,分别建立方程求解;
(3)分两种情况讨论:①当![]() 时,易得
时,易得![]() ;②当
;②当![]() 时,过点
时,过点![]() 作
作![]() 于点
于点![]() ,利用等积法求出DE,再用勾股定理求出AE,进而得到AP,用距离除以速度即可得出时间.
,利用等积法求出DE,再用勾股定理求出AE,进而得到AP,用距离除以速度即可得出时间.
解:(1)设![]() ,
,![]() ,则
,则![]() .
.
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
解得![]() ,
,
∴![]() .
.
(2)由(1)可得:![]() ,
,![]() ,
,![]() ,
,
∵动点![]() 、
、![]() 以每秒
以每秒![]() 的速度运动,时间为
的速度运动,时间为![]() ,
,
∴![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,
,
即![]() ,
,
∴![]() ;
;
②当![]() 时,
时,![]() ,
,
即![]() ,
,
∴![]() .
.
∴当![]() 的其中一边与
的其中一边与![]() 平行时,
平行时,![]() 的值为2.5秒或3秒.
的值为2.5秒或3秒.
(3)存在,分两种情况讨论:
①如图,当![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.
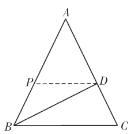
∴![]() ,
,
∴![]() ,
,
②如图,当![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.
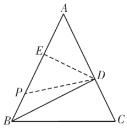
过点![]() 作
作![]() 于点
于点![]() ,
,
在![]() 中,
中,![]() ,
,
即:![]() ,
,
∴![]() ,
,
在![]() 中,
中,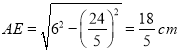 .
.
∴![]() ,
,
∴![]() .
.
综上,当![]() 的值为3或
的值为3或![]() 秒时,
秒时,![]() 是以
是以![]() 为腰的等腰三角形.
为腰的等腰三角形.


科目:初中数学 来源: 题型:
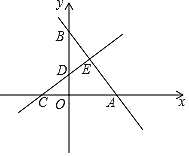
【题目】如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A、点B,直线CD与x轴、y轴分别交于点C、点D,AB与CD相交于点E,线段OA、OC的长是一元二次方程x2﹣18x+72=0的两根(OA>OC),BE=5,OB=![]() OA.
OA.
(1)求点A、点C的坐标;
(2)求直线CD的解析式;
(3)在x轴上是否存在点P,使点C、点E、点P为顶点的三角形与△DCO相似?若存在,请求出点P的坐标;如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 与双曲线
与双曲线![]() 的一个交点是
的一个交点是![]() .
.
(1)求![]() 的值;
的值;
(2)设点![]() 是双曲线
是双曲线![]() 上不同于
上不同于![]() 的一点,直线
的一点,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
①若![]() ,求
,求![]() 的值;
的值;
②若![]() ,结合图象,直接写出
,结合图象,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店参加某校读书活动,并为每班准备了A,B两套名著,赠予各班甲、乙两名优秀读者,以资鼓励.某班决定采用游戏方式发放,其规则如下:将三张除了数字2,5,6不同外其余均相同的扑克牌,数字朝下随机平铺于桌面,从中任取2张,若牌面数字之和为偶数,则甲获A名著;若牌面数字之和为奇数,则乙获得A名著,你认为此规则合理吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
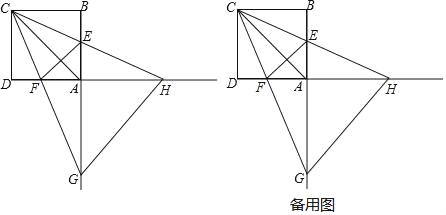
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.
查看答案和解析>>
科目:初中数学 来源: 题型:
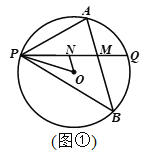
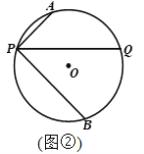
【题目】已知P是⊙O上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有动点A、B(不与P,Q重合),连接AP、BP. 若∠APQ=∠BPQ.
(1)如图1,当∠APQ=45°,AP=1,BP=2![]() 时,求⊙O的半径;
时,求⊙O的半径;
(2)如图2,选接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,若∠NOP+2∠OPN=90°,探究直线AB与ON的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图)
你选择的方案是_____(填方案一,方案二,或方案三),则B点坐标是______,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=2x与反比例函数y=![]() (k>0)的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为
(k>0)的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为![]() ,则k的值为( )
,则k的值为( )
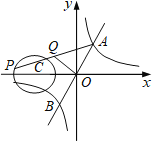
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com