
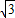 ),以点C为顶点的抛物线y=ax2+bx+c恰经过x轴上的点A,B.
),以点C为顶点的抛物线y=ax2+bx+c恰经过x轴上的点A,B.
 =2,可得点C的坐标为(2,
=2,可得点C的坐标为(2,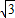 ).
).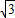 ),可设抛物线的解析式为:y=a
),可设抛物线的解析式为:y=a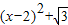
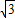 ,设平移后抛物线的解析式为y=-
,设平移后抛物线的解析式为y=-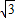 (x-2)2+k,把(0,
(x-2)2+k,把(0,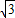 )代入上式得K=5
)代入上式得K=5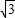 .即可得到平移后抛物线的解析式.
.即可得到平移后抛物线的解析式.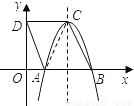 解:(1)连接AC,在菱形ABCD中,CD∥AB,
解:(1)连接AC,在菱形ABCD中,CD∥AB,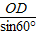 =2(2分)
=2(2分)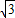 ).(3分)
).(3分)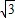 ),
),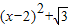
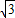 .(5分)
.(5分)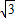 (x-2)2+k,
(x-2)2+k,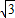 )代入上式得K=5
)代入上式得K=5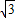 .
.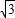 (x-2)2+5
(x-2)2+5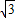 (7分)
(7分)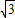 x2+4
x2+4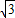 x+
x+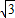 .
.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源:2009年北京市石景山区中考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2009年北京市石景山区中考数学二模试卷(解析版) 题型:解答题
 ,0),点B在第一象限,AC是∠OAB的平分线,并且与y轴交于点E,点M为直线AC上一个动点,把△AOM绕点A顺时针旋转,使边AO与边AB重合,得到△ABD.
,0),点B在第一象限,AC是∠OAB的平分线,并且与y轴交于点E,点M为直线AC上一个动点,把△AOM绕点A顺时针旋转,使边AO与边AB重合,得到△ABD. ?若存在,求出点M的坐标;若不存在,请说明理由.
?若存在,求出点M的坐标;若不存在,请说明理由.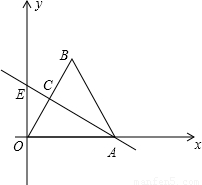
查看答案和解析>>
科目:初中数学 来源:2009年江苏省连云港市中考数学原创试卷大赛(12)(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2009年山东省日照市中考数学模拟试卷2(丁文斌)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com