练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7、下列图形中，由已知图形通过平移变换得到的是（　　）
    分析：根据平移不改变图形的形状和大小，将题中所示的图案通过平移后可以得到的图案是C．
    解答：解：观察图形可知图案C过平移后可以得到．
    故选C．
    点评：本题考查了图形的平移，图形的平移只改变图形的位置，而不改变图形的形状和大小，学生易混淆图形的平移与旋转或翻转．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    25、附加题：如图（1），把△ABC沿直线BC平行移动线段BC的长度，可以变到△DEC的位置；
    如图（2），以BC为轴，把△ABC翻折180°，可以变到△DBC的位置；
    如图（3），以点A为中心，把△ABC旋转180°，可以变到△AED的位置．
    像这样，其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的，这种只是改变位置，不改变形状大小的图形变换，叫做三角形的全等变换．

    回答下列问题：
    已知：如图（4），点E是位于正方形ABCD的边AD上一点，F为BA延长线上一点，且AF=AE；
    ①在图中，可以通过平行移动、翻折、旋转中的哪一种方法怎样变化，使△ABE变到△ADF的位置；
    ②指出图（4）中线段BE与DF之间的关系，为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

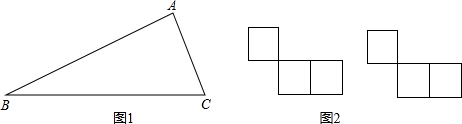
    （1）已知△ABC（如图1），求作一点P，使P到AB、AC的距离相等．（尺规作图，保留痕迹，不写作法）
    （2）下列两图（如图2）是由三个小正方形组成的图形，请你分别在图中补画一个小正方形，使补画后的两图都是轴对称图形．

    查看答案和解析>>

    科目：初中数学 来源：新课程同步练习　数学　八年级上册 题型：044

    如图，已知：AB＝AD，D是BC中点，E是AD上任意一点，连接EB、EC，求证：EB＝EC．

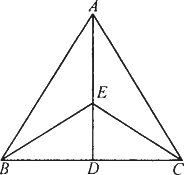
    分析：(1)观察图形，图中线段EB和线段EC是________三角形中的边．现需证EB＝EC，可证△ABE≌________或△BED≌________．

    (2)由已知可得BD＝CD，不要忽略图形中隐含的已知条件AE、DE、AD是三对全等三角形的公共边．

    (3)找需知，只需证得∠BAE＝∠CAE或∠BDE＝∠CDE，即可得到上述两个三角形全等(恰当选择SAS来判定)．

    (4)再看已知，三组对应边对应相等，可以利用SSS来证明△ABD≌△ACD，就得到∠BAE＝∠CAE或∠BDE＝∠CDE．

    请同学们完成下列填空

    证明一：∵D是BC中点　　∴BD＝CD

    在△ABD和△ACD中，

    ________

    ________

    ________

    ∴△ABD≌△ACD(SSS)

    ∴∠BAE＝∠CAE(全等三角形的对应角相等)

    在△ABE和△ACE中，

    ________

    ________

    ________

    ∴△ABE≌△ACE(SAS)

    ∴EB＝EC(全等三角形的对应边相等)

    (请同学们根据分析思路，写出第二种证明方法)

    查看答案和解析>>

    科目：初中数学 来源：黄冈难点课课练八年级数学下册（北师大版） 题型：044

    已知：下列图形都是由多个边长为1的正方形并排拼成的矩形．

    (1)如图a所示，可以算出一个正方形的对角线长为，求两个正方形并排拼成的矩形的对角线长．n个呢？

    (2)根据图b所示，求证：△BCE∽△BED；

    (3)如图c所示，在下列所给的三个结论中，通过合情推理选出一个正确的结论加以证明：

    ①∠BEC＋∠BDE＝；

    ②∠BEC＋∠BED＝；

    ③∠BEC＋∠DFE＝；

    (4)在图c中不添加辅助线和其他字母，你能否发现新的结论，如能，请加以证明．

    查看答案和解析>>

    科目：初中数学 来源：同步题 题型：单选题

    下列由若干个单位立方体搭成的几何体中，从左边看到的图形是已知图的为
    [     ]

    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案