
【题目】如图,在△ABC中,∠C=45°,∠BAC=90°,点A为( ![]() ,0)、点B为(0,1),坐标系内有一动点P,使得以P、A、C为顶点的三角形和△ABC全等,则P点坐标为 .
,0)、点B为(0,1),坐标系内有一动点P,使得以P、A、C为顶点的三角形和△ABC全等,则P点坐标为 . 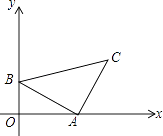
【答案】(1, ![]() +1),(2
+1),(2 ![]() ,﹣1),(2
,﹣1),(2 ![]() +1,
+1, ![]() ﹣1)
﹣1)
【解析】解:∵点A坐标为( ![]() ,0)、点B坐标为(0,1),
,0)、点B坐标为(0,1),
∴OA= ![]() ,OB=1,
,OB=1,
∴AB= ![]() =2
=2
∵∠BAC=90°,∠ACB=45°,
∴AB=AC=2,BC=2 ![]() ,
,
△ABC与△ACP全等分为三种情况:
①如图1,延长BA到P,使AB=AP,连接CP,过P作PM⊥x轴于M,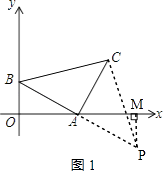
则∠AOB=∠AMP=90°
在△AOB和△AMP中,
∵ 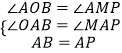 ,
,
∴△AOB≌△AMP(AAS),
∴AM=AO= ![]() ,MP=OB=1,
,MP=OB=1,
故点P的坐标为(2 ![]() ,﹣1);
,﹣1);
②如图2,过点C作CP⊥AC,使CP=AB,则△ABC≌△CPA,
故∠PAC=∠ACB=45°,AP=BC=2 ![]() ,
,
过P作PM⊥x轴于M,此时∠PAM=15°,在x轴上取一点N,使∠PNM=30°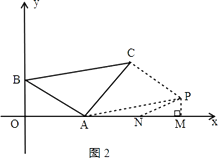
∴∠PAM=∠APN=15°,即NA=NP,
设PM=x,则PN=AN=2x,NM= ![]() x,
x,
在RT△APM中,∵AP2=AM2+PM2 ,
∴(2 ![]() )2=(2x+
)2=(2x+ ![]() x)2+x2 , 解得:x=
x)2+x2 , 解得:x= ![]() ﹣1,
﹣1,
则AM=OA+2x+ ![]() x=2
x=2 ![]() +1,
+1,
故点P的坐标为(2 ![]() +1,
+1, ![]() ﹣1);
﹣1);
③如图3,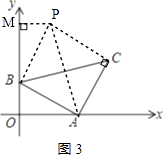
作CP⊥AC,使CP=AB,连接BP,则△ABC≌△CPA,
∵∠BAC=∠PCA=90°,且CP=AB,
∴四边形ABPC是矩形,
∴AB=BP,∠ABP=90°,即∠ABO+∠PBM=90°,
过点P作PM⊥y轴,则∠BPM+∠PBM=90°,
∴∠ABO=∠BPM,
在△AOB和△BMP中,
∵ 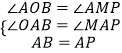 ,
,
∴△AOB≌△BMP(AAS),
∴BM=OA= ![]() ,PM=OB=1,
,PM=OB=1,
故点P的坐标为(1, ![]() +1);
+1);
综上,点P的坐标为(1, ![]() +1),(2
+1),(2 ![]() ,﹣1),(2
,﹣1),(2 ![]() +1,
+1, ![]() ﹣1).
﹣1).


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知空气的密度是1.293 kg/m3,现有一只塑料袋内装满了空气,其体积为0.0035 cm3,那么这一袋空气的质量约为多少千克?(质量=密度×体积,结果用科学记数法表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?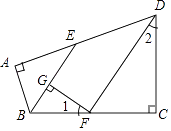
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于抛物线y=﹣(x+1)2+3,下列结论:其中正确结论的个数为( )
①抛物线的开口向下; ②对称轴为直线x=1; ③顶点坐标为(﹣1,3);④x>1时,y随x的增大而减小
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com