
| A. | 0≤a<$\frac{1}{4}$ | B. | -6≤a<0 | C. | -5<a≤$\frac{1}{4}$ | D. | -6≤a<$\frac{1}{4}$ |
分析 根据二次函数y=x2-x+a的图象与x轴的两个不同的交点得出△=b2-4ac>0,再根据原点的距离之和不超过5,得出|x1-x2|<5,进而求出即可.
解答 解:∵二次函数y=x2-x+a的图象与x轴的两个不同的交点,
∴△=b 2-4ac=1-4a>0,
解得:a<$\frac{1}{4}$,
∵图象与x轴的两个不同的交点到原点的距离之和不超过5,
∴|x1-x2|≤5,
∴x12+x22-2x1x2≤25,
∵x1+x2=1,
∴x12+x22+2x1x2=1,
x12+x22=1-2x1x2,
∴1-2x1x2-2x1x2≤25,
∴1-4x1x2≤25,
∴1-4a≤25,
∴a≥-6,
则a的取值范围是:
∴-6≤a<$\frac{1}{4}$,
故选D.
点评 此题主要考查了抛物线与x轴交点坐标的性质以及不等式组的解法等知识,根据交点个数得出△的符号以及公式变形是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形的高、中线、角平分线互相重合 | |
| B. | 顶角相等的两个等腰三角形全等 | |
| C. | 等腰三角形一边不可以是另一边的三倍 | |
| D. | 等腰三角形的两个底角相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 4.5 | D. | -4.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x}{15x+16}$ | B. | $\frac{x}{127x+128}$ | C. | $\frac{x}{255x+256}$ | D. | $\frac{x}{511x+512}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | [(a+b)2]5=(a+b)10 | B. | [(a+b)2]n=(a+b)n+2 | C. | [(a+b)x]5=(a+b)5x | D. | [(a+b)m]n=(a+b)mn |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
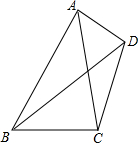 如图,四边形ABCD中,AC=6,BD=8,AC与BD所夹锐角为60°,则四边形ABCD的面积为( )
如图,四边形ABCD中,AC=6,BD=8,AC与BD所夹锐角为60°,则四边形ABCD的面积为( )| A. | 12 | B. | 12$\sqrt{3}$ | C. | 24 | D. | 24$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com