
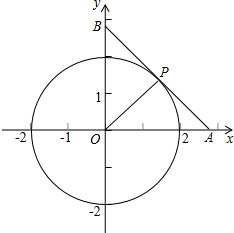
 »γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Γ―O «“‘‘≠ΒψOΈΣ‘≤–ΡΘ§ΑκΨΕΈΣ2ΒΡ‘≤Θ§P «‘ΎΒΎ“ΜœσœόΡΎΘ§Γ―O…œ“ΜΕ·ΒψΘ§ΙΐΒψPΉςΓ―OΒΡ«–œΏΖ÷±π”κxΘ§y÷αœύΫΜ”ΎΒψAΓΔBΘ°
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Γ―O «“‘‘≠ΒψOΈΣ‘≤–ΡΘ§ΑκΨΕΈΣ2ΒΡ‘≤Θ§P «‘ΎΒΎ“ΜœσœόΡΎΘ§Γ―O…œ“ΜΕ·ΒψΘ§ΙΐΒψPΉςΓ―OΒΡ«–œΏΖ÷±π”κxΘ§y÷αœύΫΜ”ΎΒψAΓΔBΘ°| 2 |
| 2 |
| 2 |
| 2 |
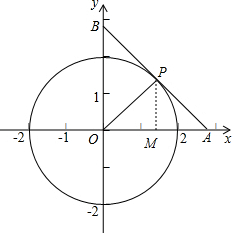 ΫβΘΚΘ®1Θ©»γΆΦΘ§ΉςPMΓΆOA”ΎΒψMΘ§
ΫβΘΚΘ®1Θ©»γΆΦΘ§ΉςPMΓΆOA”ΎΒψMΘ§| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
|
|
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
| AΓΔ12 | BΓΔ15 |
| CΓΔ12Μρ15 | DΓΔ9 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
| 1 |
| 2 |
| 8 |
| 2 |
| 2 |
| 2 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
| 2 |
| 3 |
| 3 |
| 4 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com